
 �ס�����ѧϰС�����÷�����������С��ʵ���У�������·�ֱ�ʹ����ͼ���ף������ң����ֵ����������ӷ�ʽ����֪���������RxԼΪ100������ѹ��
�ס�����ѧϰС�����÷�����������С��ʵ���У�������·�ֱ�ʹ����ͼ���ף������ң����ֵ����������ӷ�ʽ����֪���������RxԼΪ100������ѹ�� ������ԼΪ3k����������
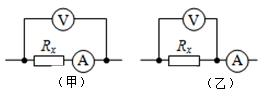
������ԼΪ3k���������� ������ԼΪ2��������ͼ���ף���ͼ���ң��е�·��õĵ���ֵ�ֱ�ΪRx1��Rx2����Rx1���Rx1����Rx2�������ӽ�����������ʵֵ���Ҳ���ֵRx1���ڣ�����ڡ��������ڡ���С�ڡ�����ʵֵ������ֵRx2С�ڣ�����ڡ��������ڡ���С�ڡ�����ʵֵ��
������ԼΪ2��������ͼ���ף���ͼ���ң��е�·��õĵ���ֵ�ֱ�ΪRx1��Rx2����Rx1���Rx1����Rx2�������ӽ�����������ʵֵ���Ҳ���ֵRx1���ڣ�����ڡ��������ڡ���С�ڡ�����ʵֵ������ֵRx2С�ڣ�����ڡ��������ڡ���С�ڡ�����ʵֵ�� ���� ���ݴ��������ֵ��������Ĺ�ϵȷ���������Ľӷ���Ȼ�����ʵ���·ͼҪ��ŷķ���ɷ���ʵ����������
��� �⣺�������֪��$\frac{{R}_{x}}{{R}_{A}}=\frac{100}{2}=50$��$\frac{{R}_{V}}{{R}_{x}}$=$\frac{3000}{100}$=30����$\frac{{R}_{x}}{{R}_{A}}$��$\frac{{R}_{v}}{{R}_{x}}$���ʵ�����Ӧ�����ڽӷ���
��Rx1���ӽ�����������ʵֵ�����ڵ����������ڽӷ�����ѹ�IJ���ֵƫ����ŷķ���ɿ�֪���������ֵ������ʵֵ��
������ͼ���õ�������ӷ������ڵ�ѹ���ķ������ö�ʹ������ʾ��ƫ������ŷķ���ɿ�֪������ֵRx2ƫС��
�ʴ�Ϊ��Rx1�����ڣ�С�ڣ�
���� ���⿼���˵������ӷ���ѡ������ʵ���������������������ֵԶ���ڵ���������ʱ������Ӧ�����ڽӷ�������ѹ������Զ���ڴ��������ֵʱ������Ӧ������ӷ���


 ��У����ϵ�д�
��У����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
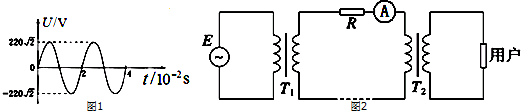
| A�� | �����E�������Ľ�����ĵ�ѹ����ʽΪe=220$\sqrt{2}$cos100��t��V�� | |
| B�� | ��������ʾ��Ϊ5A | |
| C�� | ���û����ĵĹ��ʱ��ʱ������������ĵĹ���Ҳ��� | |
| D�� | ��ֻ����T2��ԭ��Ȧ�����������������ʽ���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ��ͼ�У���֪E=220V��R1=20����R2=50����R3=30����
��ͼ�У���֪E=220V��R1=20����R2=50����R3=30�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
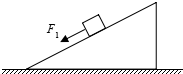 ��ͼ��ʾ��б��̶���ˮƽ���ϣ�б����һ���������б����������F1�����������»���ijʱ�����������ʩ��һ����ֱ���µĺ���F2����֮��϶̵�һ��ʱ���������˶�״̬�ǣ�������
��ͼ��ʾ��б��̶���ˮƽ���ϣ�б����һ���������б����������F1�����������»���ijʱ�����������ʩ��һ����ֱ���µĺ���F2����֮��϶̵�һ��ʱ���������˶�״̬�ǣ�������| A�� | �������»� | |
| B�� | �ȼ����»� | |
| C�� | �ȼ����»� | |
| D�� | ��ȷ��������Ӵ���Ħ��ϵ���Ĵ�С�й� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
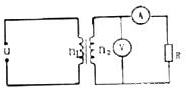 ��ͼ��ʾ�������ѹ��ԭ��Ȧ�������ѹu=1000$\sqrt{2}$sin200��t��V������ѹ������Ȧ��һ����ֵ����R=100����������ѹ��ԭ������Ȧ������n1��n2=10��1����ѹ���͵������������뽻����������˵����ȷ���ǣ�������
��ͼ��ʾ�������ѹ��ԭ��Ȧ�������ѹu=1000$\sqrt{2}$sin200��t��V������ѹ������Ȧ��һ����ֵ����R=100����������ѹ��ԭ������Ȧ������n1��n2=10��1����ѹ���͵������������뽻����������˵����ȷ���ǣ�������| A�� | ���˵�ѹΪ���ҽ����ѹ��������T=O.02s | |
| B�� | ��ѹ����ʾ��Ϊ100V����������ʾ��Ϊ1OA | |
| C�� | ��ѹ����ʾ��ΪI00��v����������ʾ��Ϊ1O$\sqrt{2}$A | |
| D�� | ����R���ĵĵ繦��Ϊ100W |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
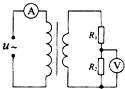 ͼ�������ѹ����ԭ������Ȧ����֮��Ϊ2��l������R1=R2=10�����������Ϊ���뽻���������R1���˵�ѹ˲ʱֵ����ʽΪu1=10$\sqrt{2}$sin100��t��V����������˵����ȷ���ǣ�������
ͼ�������ѹ����ԭ������Ȧ����֮��Ϊ2��l������R1=R2=10�����������Ϊ���뽻���������R1���˵�ѹ˲ʱֵ����ʽΪu1=10$\sqrt{2}$sin100��t��V����������˵����ȷ���ǣ�������| A�� | ��������ʾ��Ϊ0.5A | B�� | ��ѹ��ʾ��Ϊ14.14V | ||
| C�� | R1���ĵĹ���Ϊ20W | D�� | ԭ��Ȧ���뽻����Ƶ��Ϊ100Hz |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ�������ֱ�ΪM��m�����������ֱ�ᵯ����������ˮƽ���ϴ��ھ�ֹ״̬���ֽ�m��ֱ����ѹ������һ�ξ�����ɾ�ֹ�ͷţ���m������ߵ�ʱ��Mǡ�öԵ�����ѹ������֪���ɾ���ϵ��Ϊk�������α�ʼ���ڵ������ڣ��������ٶ�Ϊg��������
��ͼ��ʾ�������ֱ�ΪM��m�����������ֱ�ᵯ����������ˮƽ���ϴ��ھ�ֹ״̬���ֽ�m��ֱ����ѹ������һ�ξ�����ɾ�ֹ�ͷţ���m������ߵ�ʱ��Mǡ�öԵ�����ѹ������֪���ɾ���ϵ��Ϊk�������α�ʼ���ڵ������ڣ��������ٶ�Ϊg��������| A�� | ��m������ߵ�ʱ��m�ļ��ٶ�Ϊ$��1+\frac{M}{m}��g$ | |
| B�� | ��m������ߵ�ʱ��M�ļ��ٶ�Ϊg | |
| C�� | ��m�ٶ����ʱ�����ɵ��α���Ϊ$\frac{Mg}{k}$ | |
| D�� | ��m�ٶ����ʱ��M�Ե����ѹ��ΪMg |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 �ҹ�����ԱҪ�����1�ź�����ʵ��յ������ϲ�����������������õķ������£�����Ϊm1�ı���A��ǰ��������������Ϊm2������������������������������B�����ں����ϣ���ijһ�����������������������˶�����ͼ��ʾ���ȶ������Aǰ�������������Ķ����ֱ�ΪF1��F2���ɴ˿�֪��������B������Ϊ��������
�ҹ�����ԱҪ�����1�ź�����ʵ��յ������ϲ�����������������õķ������£�����Ϊm1�ı���A��ǰ��������������Ϊm2������������������������������B�����ں����ϣ���ijһ�����������������������˶�����ͼ��ʾ���ȶ������Aǰ�������������Ķ����ֱ�ΪF1��F2���ɴ˿�֪��������B������Ϊ��������| A�� | $\frac{{F}_{1}��{m}_{1}+2{m}_{2}��}{{F}_{1}-{F}_{2}}$ | B�� | $\frac{{F}_{2}��{m}_{1}+2{m}_{2}��}{{F}_{1}-{F}_{2}}$ | ||
| C�� | $\frac{{F}_{2}��{m}_{1}+2{m}_{2}��}{{F}_{1}}$ | D�� | $\frac{{F}_{2}��{m}_{1}+2{m}_{2}��}{{F}_{2}}$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com