
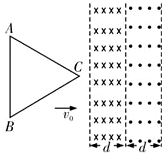
 ���Ⱦ�Ϊd���㹻�������������������ڣ������ڴŸ�Ӧǿ�ȴ�С��ΪB�������෴����ǿ�ų�������ΪR���߳�Ϊ$\frac{4\sqrt{3}}{3}$d�ĵȱ������ν������AB����ų��߽�ƽ�У��������ͼʾλ���Դ�ֱ��AB�����ҵķ���������ֱ���˶���ȡ��ʱ�뷽�����Ϊ�����ӽ�����C�˸ս���ų���ʼ��ʱ�����в����ĸ�Ӧ������ʱ��仯��ͼ���ǣ�������
���Ⱦ�Ϊd���㹻�������������������ڣ������ڴŸ�Ӧǿ�ȴ�С��ΪB�������෴����ǿ�ų�������ΪR���߳�Ϊ$\frac{4\sqrt{3}}{3}$d�ĵȱ������ν������AB����ų��߽�ƽ�У��������ͼʾλ���Դ�ֱ��AB�����ҵķ���������ֱ���˶���ȡ��ʱ�뷽�����Ϊ�����ӽ�����C�˸ս���ų���ʼ��ʱ�����в����ĸ�Ӧ������ʱ��仯��ͼ���ǣ�������| A�� | 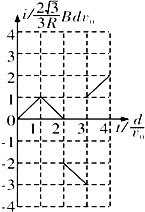 | B�� | 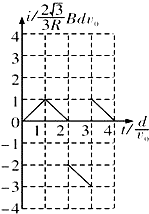 | C�� | 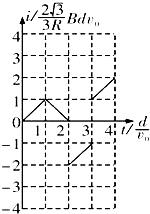 | D�� | 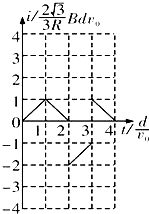 |
���� �������˶��ɷֶ��жϣ������ų������з�����������ζ��ɿ��жϵ�·�и�Ӧ�����ķ����ɵ����и�Ÿ���ʱ�ĸ�Ӧ�綯�ƹ�ʽ����ø�Ӧ�綯�ƵĴ�С����ŷķ���ɷ�����Ӧ������С�ı仯��
��� �⣺��������Ȧ�ĸ�Ϊ2d�����ڿ�ʼ�˶���0��d�����У���Ӧ������I1=$\frac{B•\frac{2\sqrt{3}}{3}dv}{R}$=$\frac{2\sqrt{3}Bdv}{3R}$��
����Ϊ��ʱ�뷽����d��2dʱ��
��ijʱ����Ȧ�����Ҳ�����ľ���Ϊx������Ȧ�и�Ÿ�Ӧ�ߵ���Ч����ΪL=$\frac{2\sqrt{3}}{3}��d-x��$��
���Ӧ����I2=$\frac{B\frac{2\sqrt{3}}{3}��d-x��v}{R}$=$\frac{2\sqrt{3}B��d-x��v}{3R}$������Ϊ��ʱ�뷽��
��x=dʱ��I=0������Ȧ��C������ұ߽�xʱ��
������L��=$\frac{4\sqrt{3}d}{3}-\frac{2\sqrt{3}}{3}��d-x��+\frac{2\sqrt{3}}{3}d$=$\frac{2\sqrt{3}}{3}��2d+��$��
��Ӧ����I3=$\frac{B\frac{2\sqrt{3}}{3}��2d+x��v}{R}$=$\frac{2\sqrt{3}B��2d+x��v}{3R}$������˳ʱ�뷽��
��x=0ʱ��I3=2$\frac{2\sqrt{3}Bdv}{3R}$��
��x=dʱ��I3=3$\frac{2\sqrt{3}Bdv}{3R}$����C������ұ߽�d��2dʱ��
������L��=$\frac{4\sqrt{3}}{3}d-\frac{2\sqrt{3}}{3}��2d-x��=\frac{2\sqrt{3}}{3}x$��
��Ӧ����I4=$\frac{B\frac{2\sqrt{3}}{3}xv}{R}$=$\frac{2\sqrt{3}Bxv}{3R}$��������ʱ�뷽��
��x=dʱ��I4=$\frac{2\sqrt{3}Bdv}{3R}$��
��x=2dʱ��I4=2$\frac{2\sqrt{3}Bdv}{3R}$����A��ȷ��BCD����
��ѡ��A��
���� ����Ϊѡ���⣬�����̱Ƚϸ��ӣ��ʿ�ѡ���ų���������������Խ�Լһ����ʱ�䣻������ڶ��δų��ִ����ų�����Ȧ�����ֲ����ĵ�����ͬ������Ч�����Ǿ��ȱ��ģ�ע���ܸ�Ӧ�綯�ƺ�ʱ���и��Ӧ�綯��֮�ͣ���ʱ���и��Ӧ�綯��֮�



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 �ҹ���2013��12��2�ճɹ����䡰�϶����š�̽��������ʵ�����ҹ��������״��ڵ�����������½��Ѳ��̽����ͼ2�ǡ��϶����š�Ѳ��������½��������뾶ΪR0��������洦�������ٶ�Ϊg0�����������İ뾶֮��Ϊ$\frac{R}{{R}_{0}}$=4�������������ٶ�֮��Ϊ$\frac{g}{{g}_{0}}$=6�������������ܶ�֮��$\frac{��}{{��}_{0}}$Ϊ��������
�ҹ���2013��12��2�ճɹ����䡰�϶����š�̽��������ʵ�����ҹ��������״��ڵ�����������½��Ѳ��̽����ͼ2�ǡ��϶����š�Ѳ��������½��������뾶ΪR0��������洦�������ٶ�Ϊg0�����������İ뾶֮��Ϊ$\frac{R}{{R}_{0}}$=4�������������ٶ�֮��Ϊ$\frac{g}{{g}_{0}}$=6�������������ܶ�֮��$\frac{��}{{��}_{0}}$Ϊ��������| A�� | $\frac{2}{3}$ | B�� | $\frac{3}{2}$ | C�� | 4 | D�� | 6 |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
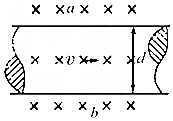 Ϊ����ϲ��˵�����ܺͶ���ѪҺ������������Ѫ����ѪҺ����������ͼ��ʾΪ���������ʾ��ͼ����Ѫ�����ڴŸ�Ӧǿ��ΪB�Ĵų��У����Ѫ������a��b������ѹΪu����֪Ѫ�ܵ�ֱ��Ϊd����Ѫ����ѪҺ������Q����λʱ���������������Ϊ��������
Ϊ����ϲ��˵�����ܺͶ���ѪҺ������������Ѫ����ѪҺ����������ͼ��ʾΪ���������ʾ��ͼ����Ѫ�����ڴŸ�Ӧǿ��ΪB�Ĵų��У����Ѫ������a��b������ѹΪu����֪Ѫ�ܵ�ֱ��Ϊd����Ѫ����ѪҺ������Q����λʱ���������������Ϊ��������| A�� | $\frac{u}{Bd}$ | B�� | $\frac{��du}{B}$ | C�� | $\frac{��du}{4B}$ | D�� | $\frac{��d2u}{4B}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ����Ϊm�Ĵ���С���þ�Ե˿��������O�㣬������ˮƽ����СΪE����ǿ�糡�У�С��ֹʱ˿������ֱ����ļн�Ϊ�ȣ���ͼ��ʾ��
����Ϊm�Ĵ���С���þ�Ե˿��������O�㣬������ˮƽ����СΪE����ǿ�糡�У�С��ֹʱ˿������ֱ����ļн�Ϊ�ȣ���ͼ��ʾ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com