
 ��ͼ��ʾ�������ȸ߹⻬��$\frac{1}{4}$Բ��������뾶Ϊr�����ΪL��������費�ƣ��ڹ����������һ��ֵΪR�ĵ��裬����װ�ô���һ��ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ��ΪB������һ�������Դ���L������Ϊ$\frac{R}{2}$������Ϊm�Ľ������ӹ�����λ��cd��ʼ���Գ��ٶ�v0���л����������պ����˶���ab�����������ٶ�Ϊg����
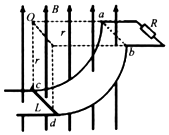
��ͼ��ʾ�������ȸ߹⻬��$\frac{1}{4}$Բ��������뾶Ϊr�����ΪL��������費�ƣ��ڹ����������һ��ֵΪR�ĵ��裬����װ�ô���һ��ֱ���ϵ���ǿ�ų��У��Ÿ�Ӧǿ��ΪB������һ�������Դ���L������Ϊ$\frac{R}{2}$������Ϊm�Ľ������ӹ�����λ��cd��ʼ���Գ��ٶ�v0���л����������պ����˶���ab�����������ٶ�Ϊg�������� ��1�����ݷ����ڵ�Ÿ�Ӧ���ɺͱպϵ�·ŷķ���ɿɵ�cd�����ĵ��Ʋ
��2�����ݷ����ڵ�Ÿ�Ӧ���ɿɵ�ƽ����Ӧ�綯�ƣ����ݱպϵ�·��ŷķ����ƽ�����������ݵ�����ļ��㹫ʽ���ͨ��R�ĵ�����
��3�����ݹ��ܹ�ϵ������������в������������ٸ��ݸ��ݽ����������R�ϲ�����������
��� �⣺��1���������ս�����ʱ�������ĸ�Ӧ�綯��Ϊ��E=BLv0��
����ŷķ���ɿɵ�cd�����ĵ��Ʋ�Ϊ��U=$\frac{E}{R+\frac{R}{2}}$��R=$\frac{2}{3}BL{v}_{0}$��
��2�����ݷ����ڵ�Ÿ�Ӧ���ɿɵ�ƽ����Ӧ�綯��Ϊ��$\overline{E}=\frac{����}{��t}$��
���ݱպϵ�·��ŷķ���ɿɵã�$\overline{I}$=$\frac{\overline{E}}{R+\frac{1}{2}R}$��
�ù�����ͨ��R�ĵ���Ϊ��q=$\overline{I}$��t=$\frac{����}{R+\frac{R}{2}}$=$\frac{2BLr}{3R}$��
��3�����ݹ��ܹ�ϵ�ɵã����������в���������Ϊ��Q��=$\frac{1}{2}m{{v}_{0}}^{2}-mgr$��
���ݽ������ɿɵ�ͨ��R�ϲ���������Ϊ��Q=$\frac{{Q}_{��}}{R+\frac{1}{2}R}•R$=$\frac{1}{3}m{v}_{0}^{2}-\frac{2}{3}mgr$��
�𣺣�1���������ս�����ʱ��cd�����ĵ��Ʋ�Ϊ$\frac{2}{3}BL{v}_{0}$��
��2���ù�����ͨ��R�ĵ���Ϊ$\frac{2BLr}{3R}$��
��3���ù�����R�ϲ���������Ϊ$\frac{1}{3}m{v}_{0}^{2}-\frac{2}{3}mgr$��
���� ���ڵ�Ÿ�Ӧ�����о�˼·������������һ�������ĽǶȣ��ص��Ƿ��������������������ƽ�����⣻��һ����������������Ÿ�Ӧ�����е��������ת���ǹؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
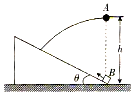 ��ͼ��ʾ����ˮƽ��������һ���Ϊ�ȵĹ⻬�̶�б�棬��б��˵����Ϸ��߶�Ϊh��ƽ��һС��A��ͬʱ��б���һ���B��ijһ���ٶ���б���ϻ������们����ߵ�ʱǡ����С��A������С��A�����B����Ϊ�ʵ㣬���Կ����������������ٶ�Ϊg���������ж���ȷ���ǣ�������
��ͼ��ʾ����ˮƽ��������һ���Ϊ�ȵĹ⻬�̶�б�棬��б��˵����Ϸ��߶�Ϊh��ƽ��һС��A��ͬʱ��б���һ���B��ijһ���ٶ���б���ϻ������们����ߵ�ʱǡ����С��A������С��A�����B����Ϊ�ʵ㣬���Կ����������������ٶ�Ϊg���������ж���ȷ���ǣ�������| A�� | ���B��б���ϻ��ij��ٶ�Ϊ$\sqrt{\frac{si{n}^{2}��}{1+sin��}2gh}$ | |
| B�� | ���B��б���ϻ��ĸ߶�$\frac{si{n}^{2}��}{1+si{n}^{2}��}$h | |
| C�� | С��A�ڿ����˶���ʱ��Ϊ$\sqrt{\frac{2h}{g}}$ | |
| D�� | С��Aˮƽ�׳�ʱ�ij��ٶ�Ϊsin��cos��$\sqrt{\frac{gh}{2��1+si{n}^{2}�ȣ�}}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �����ܵ����������Ǿ�˵��������������˹� | |
| B�� | ������������ķ�������λ�ƣ����Ǿ�˵��������������˹� | |
| C�� | ������ķ����������˶������෴������������������ | |
| D�� | ������ķ���ʼ�պ��˶�����ֱ�����������岻���� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ��ͼ����ʾ��ƽ�������д�ֱ��ֽ���������ǿ�ų���ֽ���ڵ����������߿�abcd�����������´�ͼʾλ���ɾ�ֹ��ʼ����ͨ����ǿ�ų���ab��ʼ��������ƽ�У��߿��в����ĸ�Ӧ������ʱ��仯�Ĺ�������ͼ��ʾ����֪�߿�ı߳�ΪL=0.1m���ܵ���Ϊ1����������˵����ȷ���ǣ�������
��ͼ����ʾ��ƽ�������д�ֱ��ֽ���������ǿ�ų���ֽ���ڵ����������߿�abcd�����������´�ͼʾλ���ɾ�ֹ��ʼ����ͨ����ǿ�ų���ab��ʼ��������ƽ�У��߿��в����ĸ�Ӧ������ʱ��仯�Ĺ�������ͼ��ʾ����֪�߿�ı߳�ΪL=0.1m���ܵ���Ϊ1����������˵����ȷ���ǣ�������| A�� | �߿����ų�������ͨ���߿����ĵ���Ϊ3��10-3C | |
| B�� | ��ǿ�ų��ĴŸ�Ӧǿ��Ϊ0��lT | |
| C�� | ab�߸�Ҫ���ų�ʱ���ٶȴ�СΪ1m/s | |
| D�� | �߿���ų����õ�ʱ��ԼΪ0.93s |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
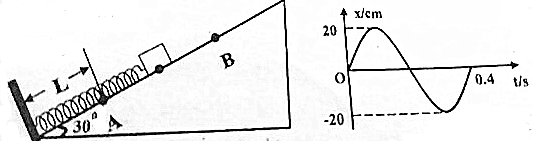
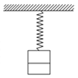 ��ͼ��ʾ����ֱ���ҵĵ������������ΪA�ļ�г�˶��������嵽����͵�ʱ������ǡ�õ���һ�루��������������һ�룩���˺���ϵͳ������ı仯Ϊ��������
��ͼ��ʾ����ֱ���ҵĵ������������ΪA�ļ�г�˶��������嵽����͵�ʱ������ǡ�õ���һ�루��������������һ�룩���˺���ϵͳ������ı仯Ϊ��������| A�� | ������� | B�� | ������ | ||
| C�� | �����С | D�� | ��������������ȷ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | m��u1+u2������ | B�� | m��u1-u2�� ���� | C�� | m��u1+u2������ | D�� | m ��u1-u2������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ��ų��ɷ���������Զ���Ĵ������ǵ�Ų� | |
| B�� | ��Ų������Ĺ��̾������������Ĺ��� | |
| C�� | ��Ų��еĵ糡���ų�����ʹ������������ഹֱ | |
| D�� | �κα仯�ĵ糡��Χ�ռ�һ��������仯�Ĵų� |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com