
 如图所示,长为L质量为M的圆柱形木棒竖直放置,在其顶部套一质量为m的铁质圆环,设铁环与木棒发生相对滑动时,彼此间有大小恒为kmg(k>1)的滑动摩擦力,现突然在木棒下端对木棒施加一个很大的冲击力,使木棒瞬间获得一个竖直向上的速度v0,
如图所示,长为L质量为M的圆柱形木棒竖直放置,在其顶部套一质量为m的铁质圆环,设铁环与木棒发生相对滑动时,彼此间有大小恒为kmg(k>1)的滑动摩擦力,现突然在木棒下端对木棒施加一个很大的冲击力,使木棒瞬间获得一个竖直向上的速度v0,分析 (1)分别取木棒和铁环为研究对象,根据牛顿第二定律求解两者加速度的大小
(2)从开始相对滑动到木棒达到最大高度有两个过程,即:从开始滑动到相对静止和相对静止到木棒达到最大高度,两过程中木棒的加速度发生了变化,应分段处理
(3)从开始相对滑动到两者速度相等,铁环和木棒有相对运动,当两者相对静止后一起做上抛运动,直至落地前无相对滑动,故木棒的最短长度应为从开始相对滑动到两者相对静止的过程中木棒和铁环上升的高度差
解答 解:(1)设M与m的加速度的大小分别为a1、a2,分别取M、m为研究对象,由牛顿第二定律可得:
Mg+kmg=Ma1
kmg-mg=ma2
解得:
${a}_{1}=\frac{M+km}{M}g$,方向竖直向下
a2=(k-1)g,方向竖直向上
(2)设从开始到相对静止,经历的时间为t,两者的速度为v,木棒上升的高度为h1,则根据运动学公式有:
v0-a1t=a2t,解得:$t=\frac{{v}_{0}}{{a}_{1}+{a}_{2}}=\frac{M{v}_{0}}{k(M+m)g}$
${h}_{1}={v}_{0}t-\frac{1}{2}{a}_{1}{t}^{2}$,解得:${h}_{1=}\frac{M(2kM+km-M){v}_{0}^{2}}{2g{k}^{2}(M+m)^{2}}$
v=a2t,解得:$v=\frac{{M(k-1)v}_{0}}{k(M+m)}$
设两者相对静止后上升的高度为h2,以系统为研究对象,由运动学公式得:
${h}_{2}=\frac{{v}_{\;}^{2}}{2g}=\frac{{M}^{2}(k-1)^{2}{v}_{0}^{2}}{2g{k}^{2}(M+m)^{2}}$
所以,木棒上升的总高度为:$h={h}_{1}+{h}_{2}=\frac{M(kM+m){v}_{0}^{2}}{2gk(M+m)^{2}}$
(3)设从开始到刚好相对静止的过程中铁环上升的高度为h3,取铁环为研究对象,根据运动学公式可得:
${h}_{3}=\frac{{v}^{2}}{2{a}_{2}}=\frac{(k-1){M}^{2}}{2{k}^{2}(M+m)^{2}g}$
此后,两者相对静止做上抛运动,直至落地前无相对滑动,所以木棒的长度L不应h1-h3,即:
L≥$\frac{M{v}_{0}^{2}}{2gk(M+m)}$
答:
(1)开始相对滑动时,木棒和铁环的加速度大小分别为$\frac{M+km}{M}g、(k-1)g$
(2)木棒上升的最大高度为$\frac{M(kM+m){v}_{0}^{2}}{2gk(M+m)^{2}}$
(3)若要求铁环在木棒下端落地前不滑离木棒,该木棒的长度至少为$\frac{M{v}_{0}^{2}}{2gk(M+m)}$
点评 (1)此题考查了牛顿第二定律和多过程问题的处理方法
(2)从开始相对滑动到两者相对静止过程中木棒做减速运动,铁环做加速度运动;相对静止后两者一直相对静止,直至落地是解决(2)、(3)两问的关键


科目:高中物理 来源: 题型:选择题
 如图所示,一列简谐横波沿x轴正方向传播,在t1=0时刻波传播到x=2.0m处的质点C.在t2=0.1s时刻,x=1.0m处的质点B第一次运动到负方向最大位移处,则( )
如图所示,一列简谐横波沿x轴正方向传播,在t1=0时刻波传播到x=2.0m处的质点C.在t2=0.1s时刻,x=1.0m处的质点B第一次运动到负方向最大位移处,则( )| A. | 质点C开始振动时的运动方向沿y轴负方向 | |
| B. | 该简谐横波的波速等于5m/s | |
| C. | 在t1~t2时间内,质点B通过的路程为4.0cm | |
| D. | 在t2时刻,这列波刚好传播到位于x=3.0m处的质点D |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 一定质量的物体,动能不变,动量一定不变 | |
| B. | 平抛物体在落地前,任意相等时间内动量变化量的大小相等,方向不同 | |
| C. | 如果在任何相等时间内物体所受合外力的冲量相等(不为零),那么该物体一定做匀变速运动 | |
| D. | 若某一个力对物体做功为零,则这个力对该物体的冲量也一定为零 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 电视机遥控器中有一半导体发光二极管,它发出频率为3.3×1014Hz的红外光,用来控制电视机的各种功能,已知这种发光二极管的发光面AB是直径为2mm的圆盘,封装在折射率n=2.5的半球形介质中,其圆心位于半球的圆形O点,如图,设真空中的光速3×108m/s.
电视机遥控器中有一半导体发光二极管,它发出频率为3.3×1014Hz的红外光,用来控制电视机的各种功能,已知这种发光二极管的发光面AB是直径为2mm的圆盘,封装在折射率n=2.5的半球形介质中,其圆心位于半球的圆形O点,如图,设真空中的光速3×108m/s.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
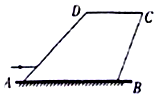 如图所示为水平面上某玻璃砖的横截面图,底边AB平行上边CD,且AB=L,∠A=45°,∠B=105°,某单色光以平行AB的方向射入玻璃砖,经过底边AB的中点反射后,最后与BC边成45°角射出,求:
如图所示为水平面上某玻璃砖的横截面图,底边AB平行上边CD,且AB=L,∠A=45°,∠B=105°,某单色光以平行AB的方向射入玻璃砖,经过底边AB的中点反射后,最后与BC边成45°角射出,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 原子是可再分的 | |
| B. | 正电荷在原子中是均匀分布的 | |
| C. | 原子中有带负电的电子,电子会对粒子有引力作用 | |
| D. | 原子的正电荷和绝大部分的质量都集中在一个很小的核上 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题

| A. | 甲、乙物体的振幅分别是2 m和1 m | |
| B. | 甲的振动频率比乙的大 | |
| C. | 前1s内两物体的加速度均为正值 | |
| D. | 第2 s末甲的速度最大,乙的加速度最小 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com