

分析 线上的A点与大圆的边缘的点具有相等的角速度,由线速度与角速度的关系求出大圆边缘的线速度;板与圆的切点具有相等的法向速度,结合它们的几何关系即可求出.
解答 解:如图,板上的C点与线轴上的C点具有相等的法向速度vn,而且板上的vn正是C点关于B轴的转动速度,则: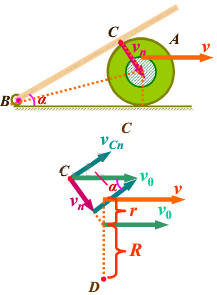
${v}_{n}=ω•\overline{BC}=ω•Rcot\frac{α}{2}$
线轴上C点的速度是C点对轴心O的转动速度vcn和与轴心相等的平动速度vo的矢量的和,而vcn是沿圆的切向的,则C点的法向速度vn应为:
vn=vo•sinα
线轴为刚体,且做纯滚动,所以以线轴与水平面的切点为基点,应有:
$\frac{v}{R+r}=\frac{{v}_{0}}{R}$
所以:${v}_{0}=\frac{R}{R+r}$
联立得:$ω=\frac{1-cosα}{R+r}$v
答:木板的角速度ω与角α的关系为$ω=\frac{1-cosα}{R+r}$v.
点评 该题为竞赛辅导题目,考查相对速度与牵连速度,因涉及的物理量与数学的关系比较多,这一类的题目历来是竞赛的难点之一,没有这方面能力的同学不需要做这一类的题目.


 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案科目:高中物理 来源: 题型:计算题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,把等边三角形ABC从垂直于它所在的平面的匀强磁场中匀速拉出,则在拉出过程中:
如图所示,把等边三角形ABC从垂直于它所在的平面的匀强磁场中匀速拉出,则在拉出过程中:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
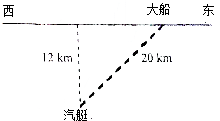 大船在海面上沿由东向西的航道以20km/h的速度航行,船西偏南某方向有一汽艇距离大船20km,距离航道12km,则汽艇速度至少为12km/h才能追到大船,若汽艇速度为15km/h,则至少要0.8h才能追上大船.
大船在海面上沿由东向西的航道以20km/h的速度航行,船西偏南某方向有一汽艇距离大船20km,距离航道12km,则汽艇速度至少为12km/h才能追到大船,若汽艇速度为15km/h,则至少要0.8h才能追上大船.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
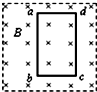 如图所示,在方向垂直纸面向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框边长ab=2L,bc=L,线框导线的总电阻为R.将线框以恒定的速度v沿垂直磁场方向移出磁场,运动中线框始终在纸面所示的平面内运动.
如图所示,在方向垂直纸面向里,磁感应强度为B的匀强磁场区域中有一个由均匀导线制成的单匝矩形线框abcd,线框边长ab=2L,bc=L,线框导线的总电阻为R.将线框以恒定的速度v沿垂直磁场方向移出磁场,运动中线框始终在纸面所示的平面内运动.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,两根平行光滑导轨竖直放置,相距L=0.1m,处于垂直轨道平面的匀强磁场中,磁感应强度B=10T,质量m=0.1kg、电阻为R=2Ω的金属杆ab接在两导轨间,在开关S断开时让ab自由下落,ab下落过程中、始终保持与导轨垂直并与之接触良好,设导轨足够长且电阻不计,取g=10m/s2,当下落h=0.8m时,开关S闭合.若从开关S闭合时开始计时,则ab下滑的速度v随时间t变化的图象是图中的( )
如图所示,两根平行光滑导轨竖直放置,相距L=0.1m,处于垂直轨道平面的匀强磁场中,磁感应强度B=10T,质量m=0.1kg、电阻为R=2Ω的金属杆ab接在两导轨间,在开关S断开时让ab自由下落,ab下落过程中、始终保持与导轨垂直并与之接触良好,设导轨足够长且电阻不计,取g=10m/s2,当下落h=0.8m时,开关S闭合.若从开关S闭合时开始计时,则ab下滑的速度v随时间t变化的图象是图中的( )| A. | 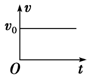 | B. |  | C. |  | D. | 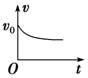 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
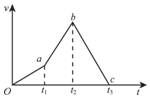
| A. | 0-t1时间内火箭的加速度小于t1-t2时间内火箭的加速度 | |
| B. | t2时刻火箭离地面最高 | |
| C. | 在0-t2时间内火箭上升,t2-t3时间内火箭下落 | |
| D. | t3时刻火箭回到地面 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com