
 ��ͼ��ʾ����ֱƽ������һ�뾶Ϊr������ΪR1����ϸ���ȵĹ⻬��Բ�ν���������M��N�������Ϊ2r�����費�Ƶ�ƽ�й⻬��������ME��NF��ӣ�EF֮����е���R2����֪R1=12R��R2=4R����MN�Ϸ���CD�·���ˮƽ�������ǿ�ų���͢Ÿ�Ӧǿ�ȴ�С��ΪB����������Ϊm�����費�Ƶĵ����ab���Ӱ�Բ������ߵ�A���ɾ�ֹ���䣬����������е����ʼ�ձ���ˮƽ�����Բ�ν�����������Ӵ����ã���ƽ�е����㹻������֪���������r/2ʱ���ٶȴ�СΪv1�����䵽MN��ʱ���ٶȴ�СΪv2��
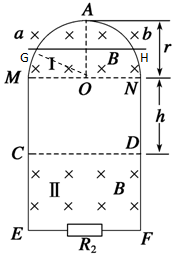
��ͼ��ʾ����ֱƽ������һ�뾶Ϊr������ΪR1����ϸ���ȵĹ⻬��Բ�ν���������M��N�������Ϊ2r�����費�Ƶ�ƽ�й⻬��������ME��NF��ӣ�EF֮����е���R2����֪R1=12R��R2=4R����MN�Ϸ���CD�·���ˮƽ�������ǿ�ų���͢Ÿ�Ӧǿ�ȴ�С��ΪB����������Ϊm�����費�Ƶĵ����ab���Ӱ�Բ������ߵ�A���ɾ�ֹ���䣬����������е����ʼ�ձ���ˮƽ�����Բ�ν�����������Ӵ����ã���ƽ�е����㹻������֪���������r/2ʱ���ٶȴ�СΪv1�����䵽MN��ʱ���ٶȴ�СΪv2������ ��1��������ܵ������Ͱ����������ã�ע���ʱ���������Ч�и�Ⱥ����·�Ĵ����������
��2�������ab����ų�II����е�����Сʼ�ղ��䣬˵������������˶��������������h�Ĺ��������ȱ���ֱ���˶��������˶����ɿ�����������h�����ݲ�����·��֪R2�����ĵĹ���ռ������·��$\frac{3}{4}$���ܵ繦�ʵ��ڵ�����������ʣ�
��3����ȷ��������������ע�ⰲ�����ı���ʽ��Ȼ�����ţ�ٵڶ�������⼴�ɣ�
��� �⣺��1���Ե����Ϊ�о������ڴų�I���и�Ÿ��ߣ����в���������Ӧ�綯�ƣ������ab��A���� 0.5rʱ��������������밲�����������������˶���
��ţ�ٵڶ����ɣ��ã�
mg-BIL=ma��
ʽ��L=$\sqrt{3}$r��I=$\frac{BL{v}_{1}}{{R}_{��}}$
�������ab����0.5rʱ���ɼ��ι�ϵ��֪����ab���ϵ�Բ���ij����ǰ�Բ���ܳ��ȵ�$\frac{2}{3}$��
����ab���ϵIJ��֣�����ֵ��8R��ab���µIJ��ֵĵ���ֵ��4R+4R��
ʽ�У�R��=$\frac{8R����4R+4R��}{8R+4R+4R}$=4R
�����ϸ�ʽ�ɵõ���a=g-$\frac{{3{B^2}{r^2}{v_1}}}{4mR}$
�ʵ����ab��A���� 0.5rʱ�ļ��ٶȴ�СΪ��a=g-$\frac{{3{B^2}{r^2}{v_1}}}{4mR}$��
��2���������abͨ���ų���ʱ����������ǡ�õ������������е�����Сʼ�ղ��䣬
����mg=BI��2r=B��$\frac{B•2r•vt}{{R}_{��}}$��2r=$\frac{4{B}^{2}{r}^{2}{v}_{t}}{{R}_{��}}$
ʽ�У�R��=$\frac{12R•4R}{12R+4R}$=3R
��ã�vt=$\frac{3mgR}{4{B}^{2}{r}^{2}}$
�������MN��CD�����ٶ�Ϊg���ȼ���ֱ���˶�����vt2-v22=2gh��
�ã�h=$\frac{{9{m^2}g{R^2}}}{{32{B^4}{r^4}}}$-$\frac{{{v_2}^2}}{2g}$
��ʱ����������Ĺ���Ϊ��PG=mgvt=$\frac{3{m}^{2}{g}^{2}R}{4{B}^{2}{r}^{2}}$��
���������غ㶨�ɣ���ʱ����������Ĺ���ȫ��ת��Ϊ��·�еĵ繦�ʣ�
��P��=P1+P2=PG=$\frac{3{m}^{2}{g}^{2}R}{4{B}^{2}{r}^{2}}$
���ԣ�P2=$\frac{3}{4}$PG=$\frac{{9{m^2}{g^2}R}}{{16{B^2}{r^2}}}$��
��3���赼���ab����ų����ʱ��t���ٶȴ�СΪv��t����ʱ��������СΪ��F��=$\frac{4{B}^{2}{r}^{2}v{��}_{t}}{3R}$
���ڵ����ab���ȼ���ֱ���˶����У�v��t=v3+at
����ţ�ٵڶ����ɣ��У�F+mg-F��=ma
����F+mg-$\frac{4{B}^{2}{r}^{2}��{v}_{3}+at��}{3R}$=ma
�����ϸ�ʽ��ã�F=$\frac{{4{B^2}{r^2}a}}{3R}$t+$\frac{{4{B^2}{r^2}{v_3}}}{3R}$+m��a-g��
�𣺣�1�������ab��A������0.5rʱ�ļ��ٶȴ�С��g-$\frac{{3{B^2}{r^2}{v_1}}}{4mR}$��
��2���ų���͢�֮��ľ���h��$\frac{{9{m^2}g{R^2}}}{{32{B^4}{r^4}}}$-$\frac{{{v_2}^2}}{2g}$��R2�ϵĵ繦��P2��$\frac{{9{m^2}{g^2}R}}{{16{B^2}{r^2}}}$��
��3����������F��ʱ��仯�Ĺ�ϵʽ��F=$\frac{{4{B^2}{r^2}a}}{3R}$t+$\frac{{4{B^2}{r^2}{v_3}}}{3R}$+m��a-g����
���� ���⿼���˹��ڵ�Ÿ�Ӧ�ĸ������⣬������������һ��Ҫ���õ��������������˶���������ܹ�ϵ���ĸ���������������


 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
Сѧ��10����Ӧ����ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
 ����Ϊ2kg�����壬����ֱƽ���ڸ�h=2.0m�Ĺ⻬���ι��A����ֹ�ع�����£�������ˮƽBC�������s=8.0m��ͣ������ȡg=10m/s2����ͼ��ʾ����
����Ϊ2kg�����壬����ֱƽ���ڸ�h=2.0m�Ĺ⻬���ι��A����ֹ�ع�����£�������ˮƽBC�������s=8.0m��ͣ������ȡg=10m/s2����ͼ��ʾ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
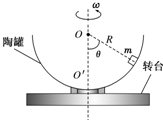 ��ͼ��ʾ���뾶ΪR�İ������չޣ��̶��ڿ�������ֱ����ת��ˮƽת̨�ϣ�ת̨ת������չ�����O�ĶԳ���OO���غϣ�ת̨��һ�����ٶȦ�������ת��һ����Ϊm��С��������չ��ڣ�����һ��ʱ���С������չ�һ��ת������Թޱھ�ֹ������O���������OO��֮��ļнǦ�Ϊ60�㣮�������ٶȴ�СΪg��
��ͼ��ʾ���뾶ΪR�İ������չޣ��̶��ڿ�������ֱ����ת��ˮƽת̨�ϣ�ת̨ת������չ�����O�ĶԳ���OO���غϣ�ת̨��һ�����ٶȦ�������ת��һ����Ϊm��С��������չ��ڣ�����һ��ʱ���С������չ�һ��ת������Թޱھ�ֹ������O���������OO��֮��ļнǦ�Ϊ60�㣮�������ٶȴ�СΪg���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ��ʱ�ٶȵĴ�С��$\sqrt{5}$v0 | |
| B�� | �˶�ʱ����$\frac{2{v}_{0}^{\;}}{g}$ | |
| C�� | �˶���λ����$\frac{2\sqrt{2}{{v}_{0}}^{2}}{g}$ | |
| D�� | ��ֱ���ٶȴ�С����ˮƽ���ٶȴ�С |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
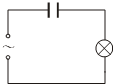 ��ͼ��ʾ��һƽ�а��������һ�����ݴ��������ڽ�����Դ�ϣ������������⣬������Щ����е��ݻ�䰵��������
��ͼ��ʾ��һƽ�а��������һ�����ݴ��������ڽ�����Դ�ϣ������������⣬������Щ����е��ݻ�䰵��������| A�� | ��С���������Ƶ�� | |
| B�� | �����������������糣��Ϊ�ŵĵ���� | |
| C�� | ��������������������� | |
| D�� | ���������������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
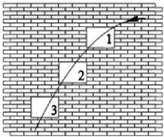 ��һֻƻ��ˮƽ�׳���ƻ���ڿ������ηɹ�������ȫ��ͬ�Ĵ���1��2��3��ͼ������Ϊƻ���ڿ������еĹ켣�����ƿ�������������˵����ȷ���ǣ�������
��һֻƻ��ˮƽ�׳���ƻ���ڿ������ηɹ�������ȫ��ͬ�Ĵ���1��2��3��ͼ������Ϊƻ���ڿ������еĹ켣�����ƿ�������������˵����ȷ���ǣ�������| A�� | ƻ��ͨ����1���������õ�ʱ��� | |
| B�� | ƻ��ͨ����3�������Ĺ����У���ֱ�����ƽ���ٶ���С | |
| C�� | ƻ��ͨ����1�������Ĺ����У������������ | |
| D�� | ƻ��ͨ����2�������Ĺ����У�������ƽ��������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
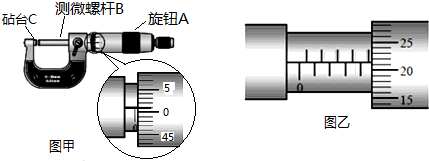
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
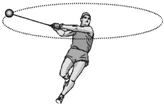 �������˶��У��˶�Աʹ���������ת����ˮƽ������Բ���˶���Ȼ��ͻȻ���֣����ڹ��ԣ�������Զ����ȥ��������Բ���˶��İ뾶ΪR��������ˮƽ������Բ���˶�ʱ����ظ߶�Ϊh����Բ���ڵ����ͶӰ��ΪO���������ص�ΪP��O��P����ľ��뼴Ϊ�˶�Ա�ijɼ������˶�Աij��������ijɼ�ΪL�������������Բ��ƣ���������˶�Ա�����ѿ�ʱ���ٶ�vΪ��������
�������˶��У��˶�Աʹ���������ת����ˮƽ������Բ���˶���Ȼ��ͻȻ���֣����ڹ��ԣ�������Զ����ȥ��������Բ���˶��İ뾶ΪR��������ˮƽ������Բ���˶�ʱ����ظ߶�Ϊh����Բ���ڵ����ͶӰ��ΪO���������ص�ΪP��O��P����ľ��뼴Ϊ�˶�Ա�ijɼ������˶�Աij��������ijɼ�ΪL�������������Բ��ƣ���������˶�Ա�����ѿ�ʱ���ٶ�vΪ��������| A�� | L$\sqrt{\frac{g}{2h}}$ | B�� | R$\sqrt{\frac{g}{2h}}$ | C�� | $\sqrt{\frac{g}{2h}��{L}^{2}-{R}^{2}��}$ | D�� | $\sqrt{\frac{g}{2h}��{L}^{2}+{R}^{2}��}$ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
 ����ֱƽ������һ���ֲڵ�$\frac{1}{4}$Բ���������뾶R=0.4m���������͵�����߶�h=0.45m��һ����m=0.1kg��С����ӹ������ߵ�A�ɾ�ֹ�ͷţ�������͵�Bʱ��һ����ˮƽ�ٶ��뿪�������ص�C������͵��ˮƽ����x=0.6m�������������ƣ�gȡ10m/s2����������ȷ���ǣ�������
����ֱƽ������һ���ֲڵ�$\frac{1}{4}$Բ���������뾶R=0.4m���������͵�����߶�h=0.45m��һ����m=0.1kg��С����ӹ������ߵ�A�ɾ�ֹ�ͷţ�������͵�Bʱ��һ����ˮƽ�ٶ��뿪�������ص�C������͵��ˮƽ����x=0.6m�������������ƣ�gȡ10m/s2����������ȷ���ǣ�������| A�� | С�����뿪���ʱ���ٶȴ�СΪ2.0m/s | |
| B�� | С�����˶��������͵�ʱ���Թ����ѹ����СΪ2.0N | |
| C�� | С�����ڹ�����˶��Ĺ����У��˷�Ħ���������Ĺ�Ϊ0.2J | |
| D�� | С�����䵽C��ʱ��������˲ʱ����Ϊ$\sqrt{13}$W |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com