
 如图所示,倾角为θ=37°的足够长平行导轨顶端bc间、底端ad间分别连一电阻,其阻值为R1=R2=2r,两导轨间距为L=1m.在导轨与两个电阻构成的回路中有垂直于轨道平面向下的磁场,其磁感应强度为B1=1T.在导轨上横放一质量m=1kg、电阻为r=1Ω、长度也为L的导体棒ef,导体棒与导轨始终良好接触,导体棒与导轨间的动摩擦因数为μ=0.5.在平行导轨的顶端通过导线连接一面积为S=0.5m2、总电阻为r、匝数N=100的线圈(线圈中轴线沿竖直方向),在线圈内加上沿竖直方向,且均匀变化的磁场B2(图中未画),连接线圈电路上的开关K处于断开状态,g=10m/s2,不计导轨电阻.
如图所示,倾角为θ=37°的足够长平行导轨顶端bc间、底端ad间分别连一电阻,其阻值为R1=R2=2r,两导轨间距为L=1m.在导轨与两个电阻构成的回路中有垂直于轨道平面向下的磁场,其磁感应强度为B1=1T.在导轨上横放一质量m=1kg、电阻为r=1Ω、长度也为L的导体棒ef,导体棒与导轨始终良好接触,导体棒与导轨间的动摩擦因数为μ=0.5.在平行导轨的顶端通过导线连接一面积为S=0.5m2、总电阻为r、匝数N=100的线圈(线圈中轴线沿竖直方向),在线圈内加上沿竖直方向,且均匀变化的磁场B2(图中未画),连接线圈电路上的开关K处于断开状态,g=10m/s2,不计导轨电阻.分析 (1)当导体棒加速度为零时,速度最大,结合切割产生的感应电动势公式、闭合电路欧姆定律和安培力公式求出导体棒的最大速度.
(2)根据电阻R1上产生的焦耳热得出整个回路产生的焦耳热,结合动能定理,抓住克服安培力做功等于整个回路产生的焦耳热,求出导体棒下滑的距离.
(3)当安培力较大时,导体棒所受的摩擦力沿斜面向下,当安培力较小时,导体棒所受的摩擦力沿斜面向上,抓住临界状态,结合平衡,以及法拉第电磁感应定律,串并联电路的特点求出磁感应强度变化率的范围.
解答 解:(1)对导体棒,由牛顿第二定律有mgsinθ-μmgcosθ-BIL=ma ①
其中I=$\frac{E}{{R}_{总}}=\frac{BLv}{r+\frac{2r}{2}}=\frac{BLv}{2r}$,②
由①②知,随着导体棒的速度增大,加速度减小,当加速度减至0时,导体棒的速度达最大vm,有:
${v}_{m}=\frac{2mgr(sinθ-μcosθ)}{{B}^{2}{L}^{2}}$,
代入数据解得vm=4m/s ③
(2)导体棒从静止释放到稳定运行之后的一段时间内,由动能定理有
mgsinθ•d-μmgcosθ•d-W克安=$\frac{1}{2}m{{v}_{m}}^{2}$,④
根据功能关系有:W克安=E电=Q总,⑤
根据并联电路特点得,Q总=4Q ⑥
由③④⑤⑥联立得d=5m.
(3)开关闭合后,导体棒ef受到的安培力F′=B1IefL ⑧
干路电流$I′=\frac{E′}{{R}_{总}}=\frac{1}{{R}_{总}}•N\frac{△Φ}{△t}=\frac{NS}{{R}_{总}}•\frac{△{B}_{2}}{△t}$ ⑨
电路的总电阻${R}_{总}=r+\frac{1}{\frac{1}{r}+\frac{1}{2r}+\frac{1}{2r}}=\frac{3}{2}r$ ⑩
根据电路规律及⑨⑩得${I}_{ef}=\frac{△{B}_{2}}{△t}•\frac{NS}{3r}$⑪
由⑧⑪联立得$\frac{△{B}_{2}}{△t}=\frac{F′•3r}{N{B}_{1}LS}$⑫
当安培力较大时Fmax=mgsinθ+μmgcosθ=10N⑬
由⑫⑬解得$(\frac{△{B}_{2}}{△t})_{max}=0.6T/s$⑭
安培力较小时Fmin=mgsinθ-μmgcosθ=2N⑮
由⑫⑮得$(\frac{△{B}_{2}}{△t})_{min}=0.12T/s$⑯
为使导体棒静止于倾斜导轨上,磁感应强度的变化的取值范围为:$0.12T/s≤\frac{△{B}_{2}}{△t}≤0.60T/s$.
根据楞次定律和安培定则知闭合线圈中所加磁场:若方向竖直向上,则均匀减小;若方向竖直向下,则均匀增强.
答:(1)从静止释放导体棒,导体棒能达到的最大速度是4m/s;
(2)导体下滑的距离是5m;
(3)在线圈中所加磁场的磁感应强度若方向竖直向上,则均匀减小;若方向竖直向下,则均匀增强.$\frac{△{B}_{2}}{△t}$大小的取值范围为$0.12T/s≤\frac{△{B}_{2}}{△t}≤0.60T/s$.
点评 本题考查了电磁感应与力学和能量的综合运用,知道导体棒加速度为零时,速度最大,知道克服安培力做功等于整个回路产生的热量,对于第三问,实质是共点力平衡的运用,通过法拉第电磁感应定律和欧姆定律、安培力公式综合求解.


 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案科目:高中物理 来源: 题型:选择题
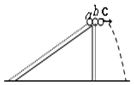 如图所示,a、b、c三个相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.下列说法正确的有( )
如图所示,a、b、c三个相同的小球,a从光滑斜面顶端由静止开始自由下滑,同时b、c从同一高度分别开始自由下落和平抛.下列说法正确的有( )| A. | 它们的落地时间相同 | |
| B. | 落地时b、c两小球重力做功的瞬时功率相等 | |
| C. | 它们的落地时的动能相同 | |
| D. | 落地时a、b两小球重力做功的瞬时功率相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,光滑水平面上有一木块,质量为M=1kg,长度1m.在木板的最左端有一个小滑块(可视为质点),质量为m=1kg.小滑块与木板之间的动摩擦因数μ=0.3.开始时它们都处于静止状态,某时刻起对小滑块施加一个F=8N水平向右的恒力,此后小滑块将相对于木板滑动,直到小滑块离开木板.g=10m/s2,求:
如图所示,光滑水平面上有一木块,质量为M=1kg,长度1m.在木板的最左端有一个小滑块(可视为质点),质量为m=1kg.小滑块与木板之间的动摩擦因数μ=0.3.开始时它们都处于静止状态,某时刻起对小滑块施加一个F=8N水平向右的恒力,此后小滑块将相对于木板滑动,直到小滑块离开木板.g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
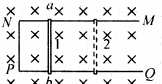 如图所示,有一U形金属导轨MNPQ,处在与它垂直的匀强磁中.有一导体棒ab在导轨上向右匀速运动,经过0.1s,从“1”位置运动到“2”位置.这个过程中,穿过由导轨和导体棒组成的闭合回路的磁通量从0.05Wb增加到0.15Wb.则这段时间内通过回路的磁通量的变化量;为0.10Wb;这段时间内线圈中的感应电动势的大小为1V.
如图所示,有一U形金属导轨MNPQ,处在与它垂直的匀强磁中.有一导体棒ab在导轨上向右匀速运动,经过0.1s,从“1”位置运动到“2”位置.这个过程中,穿过由导轨和导体棒组成的闭合回路的磁通量从0.05Wb增加到0.15Wb.则这段时间内通过回路的磁通量的变化量;为0.10Wb;这段时间内线圈中的感应电动势的大小为1V.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示为电流天平,可以用来测量匀强磁场的磁感应强度,它的右臂挂着矩形线圈,匝数为n,线圈的水平边长为L,处于匀强磁场内,磁感应强度B的方向与线圈平面垂直,当线圈中通过电流I时,调节砝码使两臂达到平衡,然后使电流反向,大小不变,这时需要在左盘中增加质量为m的砝码,才能使两臂达到新的平衡.重力加速度为g,则线圈所在位置处磁感应强度B的大小是( )
如图所示为电流天平,可以用来测量匀强磁场的磁感应强度,它的右臂挂着矩形线圈,匝数为n,线圈的水平边长为L,处于匀强磁场内,磁感应强度B的方向与线圈平面垂直,当线圈中通过电流I时,调节砝码使两臂达到平衡,然后使电流反向,大小不变,这时需要在左盘中增加质量为m的砝码,才能使两臂达到新的平衡.重力加速度为g,则线圈所在位置处磁感应强度B的大小是( )| A. | $\frac{mg}{IL}$ | B. | $\frac{mg}{nIL}$ | C. | $\frac{mg}{2IL}$ | D. | $\frac{mg}{2nIL}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 安培是电磁学中 基本物理量电流的国际单位,也是国际单位制中七个基本单位之一 | |
| B. | 安培提出分子电流假说,揭示了磁现象是由运动的电荷产生的 | |
| C. | 安培力是洛伦兹力的宏观表现,洛伦兹力是安培力的微观解释 | |
| D. | 安培定则也叫右手定则,常用来判断运动导线切割磁感线所产生感应电动势的方向 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
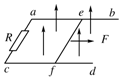 如图所示,abcd为静止于水平面上宽度为L而长度足够长的U型金属滑轨,ac边接有电阻R,其他部分电阻不计.ef为一可在滑轨平面上滑动、质量为m的均匀导体棒.整个滑轨面处在竖直向上的匀强磁场中,磁感应强度为B.忽略所有摩擦.若用恒力F沿水平方向向右拉棒,使其平动,求导体棒的最大速度.
如图所示,abcd为静止于水平面上宽度为L而长度足够长的U型金属滑轨,ac边接有电阻R,其他部分电阻不计.ef为一可在滑轨平面上滑动、质量为m的均匀导体棒.整个滑轨面处在竖直向上的匀强磁场中,磁感应强度为B.忽略所有摩擦.若用恒力F沿水平方向向右拉棒,使其平动,求导体棒的最大速度.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
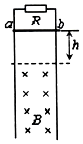 如图所示,两足够长的光滑金属直轨道竖直固定,间距为l=1m,上端与阻值为R=0.2Ω的电阻相连,在轨道平面虚线的下方,有磁感应强度为B=1T,方向垂直纸面向里的匀强磁场.一质量为m=0.2kg,电阻r=0.8Ω的金属杆ab在距离磁场边界的上方h=0.8m处由静止释放,金属杆下落过程中始终保持水平且与竖直金属轨道接触良好,不计金属轨道的电阻和空气阻力,重力加速度为g.求:
如图所示,两足够长的光滑金属直轨道竖直固定,间距为l=1m,上端与阻值为R=0.2Ω的电阻相连,在轨道平面虚线的下方,有磁感应强度为B=1T,方向垂直纸面向里的匀强磁场.一质量为m=0.2kg,电阻r=0.8Ω的金属杆ab在距离磁场边界的上方h=0.8m处由静止释放,金属杆下落过程中始终保持水平且与竖直金属轨道接触良好,不计金属轨道的电阻和空气阻力,重力加速度为g.求:查看答案和解析>>
科目:高中物理 来源: 题型:实验题
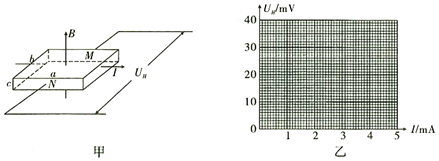
| I(mA) | 1.3 | 2.2 | 3.0 | 3.7 | 4.4 |
| UH (mV) | 10.2 | 17.3 | 23.6 | 29.1 | 34.6 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com