
分析 (1)第一宇宙速度是近地飞行的卫星的运行速度,根据万有引力提供回击运动向心力和星球表面重力万有引力相等求得星球的第一宇宙速度;
(2)根据重力与万有引力相等求得“高锟星”的质量,再根据密度公式求得该星的密度;
(3)根据万有引力提供圆周运动向心力由卫星运行的周期和星球的质量求得卫星距该星表面的高度.
解答 解:(1)第一宇宙速度时近地卫星的运行速度,满足万有引力提供圆周运动向心力,而在星球表面重力与万有引力相等有:
$G\frac{mM}{{R}^{2}}=mg=m\frac{{v}_{1}^{2}}{R}$
可得卫星环绕“高锟星”运行的第一宇宙速度为:${v}_{1}=\sqrt{gR}$;
(2)根据星球表面重力与万有引力相等有:$G\frac{mM}{{R}^{2}}=mg$
可得高锟星的质量为:M=$\frac{g{R}^{2}}{G}$
根据密度公式有,该星的平均速度为:$ρ=\frac{M}{V}=\frac{\frac{g{R}^{2}}{G}}{\frac{4}{3}π{R}^{3}}$=$\frac{3g}{4πGR}$;
(3)设高锟星质量为M,卫星质量为m,轨道半径r,
根据题意有:$G\frac{mM}{{r}^{2}}=m\frac{4{π}^{2}}{{T}^{2}}r$
由(2)得:M=$\frac{g{R}^{2}}{G}$
所以可得卫星的轨道半径为:r=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$
所以卫星距地面高度为:h=r-R=$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R
答:(1)卫星环绕“高锟星”运行的第一宇宙速度为$\sqrt{gR}$;
(2)假设“高锟星”为一均匀球体,“高锟星”的平均密度为$\frac{3g}{4πGR}$;
(3)假设某卫星绕“高锟星”做匀速圆周运动且运行周期为T,该卫星距地面的高度$\root{3}{\frac{g{R}^{2}{T}^{2}}{4{π}^{2}}}$-R.
点评 解决天体问题的两个主要入手点:一是星球表面重力与万有引力相等,二是万有引力提供环绕天体的向心力.


科目:高中物理 来源: 题型:选择题
 为了让乘客乘车更为舒适,某搡究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图所示,当此车减速上坡时(仅考虑乘客与水平面之间的作用),则关于乘客下列说法正确的是( )
为了让乘客乘车更为舒适,某搡究小组设计了一种新的交通工具,乘客的座椅能随着坡度的变化而自动调整,使座椅始终保持水平,如图所示,当此车减速上坡时(仅考虑乘客与水平面之间的作用),则关于乘客下列说法正确的是( )| A. | 不受摩擦力的作用 | B. | 受到水平向左的摩擦力作用 | ||
| C. | 处于超重状态 | D. | 所受合力竖直向上 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 月球绕地球运行的周期及月地中心间的距离 | |
| B. | 绕月球表面运行的飞船的周期及月球的半径 | |
| C. | 绕月球表面运行的飞船的周期及线速度 | |
| D. | 月球表面的重力加速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
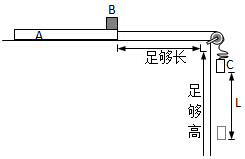 在足够高的光滑水平台面上静置一质量为m的木板A,在木板的右端静置一质量为4m可视为质点的小物体B,A、B间的滑动摩擦系数μ=0.25,且认为最大静摩擦力等于滑动摩擦力.离A右端足够远的平台边缘有一光滑定滑轮,用不可伸长的轻绳绕过定滑轮连接A和质量也为m的物体C,现由静止释放C,当它自由下落L时轻绳绷紧.当B与A相对静止时刚好到达A的左端.若重力加速度为g,不计空气阻力,不考虑A与滑轮碰撞及之后的情形.
在足够高的光滑水平台面上静置一质量为m的木板A,在木板的右端静置一质量为4m可视为质点的小物体B,A、B间的滑动摩擦系数μ=0.25,且认为最大静摩擦力等于滑动摩擦力.离A右端足够远的平台边缘有一光滑定滑轮,用不可伸长的轻绳绕过定滑轮连接A和质量也为m的物体C,现由静止释放C,当它自由下落L时轻绳绷紧.当B与A相对静止时刚好到达A的左端.若重力加速度为g,不计空气阻力,不考虑A与滑轮碰撞及之后的情形.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
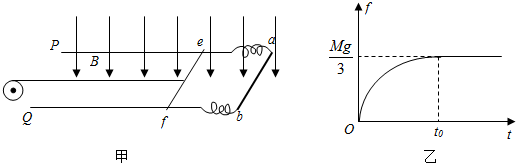
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
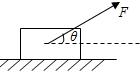 质量为m的木块在拉力F的作用下,在水平地面上做匀速运动,如图所示,已知木块与地面间的动摩擦因数为μ,那么物体受到的滑动摩擦力大小为( )
质量为m的木块在拉力F的作用下,在水平地面上做匀速运动,如图所示,已知木块与地面间的动摩擦因数为μ,那么物体受到的滑动摩擦力大小为( )| A. | μmg | B. | Fcosθ | C. | μ(mg-Fsinθ) | D. | μ(mg+Fsinθ) |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 物体A加速度大 | B. | 物体B加速度大 | C. | 物体A的速度大 | D. | 物体B的速度大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
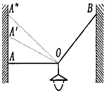 如图所示,电灯悬挂于两墙壁之间,更换水平绳oA使连接点A向上移动而保持0点的位置不变,则在A点向上移动的过程中( )
如图所示,电灯悬挂于两墙壁之间,更换水平绳oA使连接点A向上移动而保持0点的位置不变,则在A点向上移动的过程中( )| A. | 绳OB的拉力逐渐增大 | B. | 绳OB的拉力逐渐减小 | ||
| C. | 绳0A的拉力先增大后减小 | D. | 绳0A的拉力先减小后增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,木块A、B的重分别50N和60N,它们与水平地面间的动摩擦因数均为0.24,拴在木块A、B之间的轻质弹簧劲度系数为400N/m,被压缩了2cm,整个系统处于静止状态.问:
如图所示,木块A、B的重分别50N和60N,它们与水平地面间的动摩擦因数均为0.24,拴在木块A、B之间的轻质弹簧劲度系数为400N/m,被压缩了2cm,整个系统处于静止状态.问:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com