
 有一两端开口J形玻璃管,灌入一定量水银,并使管子竖直放置,中间固定一刻度尺(如图所示).某同学用该装置测定大气压强,先将左管口用橡皮帽封住,读取左管口刻度及两液面刻度,然后不断加水银,不断读取两液面刻度,得到如下一组数据.
有一两端开口J形玻璃管,灌入一定量水银,并使管子竖直放置,中间固定一刻度尺(如图所示).某同学用该装置测定大气压强,先将左管口用橡皮帽封住,读取左管口刻度及两液面刻度,然后不断加水银,不断读取两液面刻度,得到如下一组数据.| 1 | 2 | 3 | 4 | 5 | |
| 左管液面刻度(cm) | 3.0 | 3.5 | 4.0 | 4.5 | 12.5 |
| 右管液面刻度(cm) | 3.0 | 7.4 | 12.2 | 17.5 | 12.5 |
| 左管口刻度 (cm) | 13.0 | ||||
分析 (1)因等温变化的气体状态方程为P1V1=P2V2,要求的大气压强,得有两组状态参量才行,所以可知要至少测量2组数据,为了减少误差,常进行多次测量求平均的方法.
(2)根据左右管的液面的刻度,分析出各状态的状态参量,由等温变化的气体状态方程P1V1=P2V2列式求解即可得出大气压强的数值.
(3)通过左右液面的刻度判断出左边气体压强的情况,由此可判断出左管的气体的质量发生了变化,继而可知产生此现象的原因.
解答 解:(1)该过程为等温变化,有PV=恒量,即:P1V1=P2V2,所以至少要测量2组数据,才可计算出大气压强.为零减少误差,常采用的方法是多次测量求平均.
(2)设玻璃管的合计面积为S,
第一次测量时,左管空气柱的长度为:l1=13.0-3.0=10.0cm,体积为:V1=10.0S,压强为P1=P0,
第二次测量时,左管空气柱的长度为:l2=13.0-3.5=9.5cm,体积为:V2=9.5S,压强为P2=P0+(7.4-3.5)cmHg,
由等温变化得:P1V1=P2V2…①
第三次测量时,左管空气柱的长度为:l3=13.0-4.0=9.0cm,体积为:V3=9.0S,压强为P3=${P}_{0}^{′}$+(12.2-4.0)cmHg,
第四次测量时,左管空气柱的长度为:l4=13.0-4.5=8.5cm,体积为:V4=8.5S,压强为P4=${P}_{0}^{′}$+(17.5-4.5)cmHg,
由等温变化得:P3V3=P4V4…②
$\overline{{P}_{0}}$=$\frac{{P}_{0}{+P}_{0}^{′}}{2}$…③
联立①②③式并代入数据得:$\overline{{P}_{0}}$=73.9cmHg
(3)第5组数据左右两管内的液面高度相同,说明左管中的气体压强与外界的大气压相等,而气体的体积又减少了,说明左管中的气体质量减少,所以左管出现了漏气现象,或者是橡皮帽脱了等现象发生.
故答案为:(1)2,多次测量求平均值;(2)73.9;(3)漏气(或橡皮帽脱落等)
点评 该题考察了被封闭气体的等温变化,要明确计算时要涉及到两个状态;为了减少误差,常用的方法是进行多次测量求平均;该题还要注意实验的注意事项,要保证气体的质量不变和气体的温度不能变化.并会分析误差产生的原因.


科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,在光滑的水平面上有一质量为M、倾角为θ的光滑斜面,一质量为m的物块从斜面上由静止下滑.下面给出的物块在下滑过程中对斜面压力大小FN的四个表达式中,只有一个是正确的,你可能不会求解,但是你可以通过分析,对下列表达式做出合理的判断.根据你的判断,合理的表达式应为( )
如图所示,在光滑的水平面上有一质量为M、倾角为θ的光滑斜面,一质量为m的物块从斜面上由静止下滑.下面给出的物块在下滑过程中对斜面压力大小FN的四个表达式中,只有一个是正确的,你可能不会求解,但是你可以通过分析,对下列表达式做出合理的判断.根据你的判断,合理的表达式应为( )| A. | $\frac{Mmgsinθ}{M+mco{s}^{2}θ}$ | B. | $\frac{mgcosθ}{M+msi{n}^{2}θ}$ | ||
| C. | $\frac{Mmgcosθ}{m+Msi{n}^{2}θ}$ | D. | $\frac{Mmgcosθ}{M+msi{n}^{2}θ}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 一个小球沿斜面向下运动,用每隔0.1s曝一次光的频闪照相机,拍摄不同时刻的小球位置的照片如图所示,照片上出现的小球不同时间的位移见表
一个小球沿斜面向下运动,用每隔0.1s曝一次光的频闪照相机,拍摄不同时刻的小球位置的照片如图所示,照片上出现的小球不同时间的位移见表| S1/cm | S2/cm | S3/cm | S4/cm | … |
| 8.20 | 10.00 | 11.80 | 13.60 | … |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,两个光滑轨道ABC和ADE,若从轨道顶端分别静止释放两个小球,则两球离开轨道后的最高点相比较(不计阻力)( )
如图所示,两个光滑轨道ABC和ADE,若从轨道顶端分别静止释放两个小球,则两球离开轨道后的最高点相比较(不计阻力)( )| A. | 左球较高 | B. | 右球较高 | ||
| C. | 一样高 | D. | 条件不足,无法确定 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
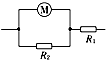 某辆以蓄电池为驱动能源的环保汽车,总质量m=3×103 kg.当它在水平路面上以v=36km/h的速度匀速行驶时,蓄电池的输出电流I=50A,输出电压U=200V.在此行驶状态下,该环保汽车能够将蓄电池输出功率的90%转化为用于牵引汽车前进的机械功率P机.(g取10m/s2)
某辆以蓄电池为驱动能源的环保汽车,总质量m=3×103 kg.当它在水平路面上以v=36km/h的速度匀速行驶时,蓄电池的输出电流I=50A,输出电压U=200V.在此行驶状态下,该环保汽车能够将蓄电池输出功率的90%转化为用于牵引汽车前进的机械功率P机.(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力可能是( )
如图所示,小车的质量为M,人的质量为m,人用恒力F拉绳,若人与车保持相对静止,且地面为光滑的,又不计滑轮与绳的质量,则车对人的摩擦力可能是( )| A. | ($\frac{M-m}{m+M}$)F,方向向左 | B. | ($\frac{m-M}{m+M}$)F,方向向右 | ||
| C. | ($\frac{m-M}{m+M}$)F,方向向左 | D. | ($\frac{M-m}{m+M}$)F,方向向右 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com