
 如图所示,虚线OL与y轴的夹角θ=45°,在OL上侧有平行于OL向下的匀强电场,在OL下侧有垂直纸面向外的匀强磁场,一质量为m、电荷量q(q>0)的粒子以速率v0从y轴上的M(OM=d)点垂直于y轴射入匀强电场,该粒子恰好能够垂直于OL进入匀强磁场,不计粒子重力.
如图所示,虚线OL与y轴的夹角θ=45°,在OL上侧有平行于OL向下的匀强电场,在OL下侧有垂直纸面向外的匀强磁场,一质量为m、电荷量q(q>0)的粒子以速率v0从y轴上的M(OM=d)点垂直于y轴射入匀强电场,该粒子恰好能够垂直于OL进入匀强磁场,不计粒子重力.分析 (1)根据粒子只受电场力作用,沿电场线方向和垂直电场线方向建立坐标系,利用类平抛运动;根据横向位移及纵向速度建立方程组,即可求解;
(2)由(1)求出在电场中运动的时间及离开电场时的位置;再根据粒子在磁场中做圆周运动,由圆周运动规律及几何关系得到最大半径,进而得到最长时间;
解答  解:(1)粒子在电场中运动,不计粒子重力,只受电场力作用,F电=qE,$a=\frac{qE}{m}$;
解:(1)粒子在电场中运动,不计粒子重力,只受电场力作用,F电=qE,$a=\frac{qE}{m}$;
沿垂直电场线方向X和电场线方向Y建立坐标系,
则在X方向位移关系有:dsinθ=v0cosθ•t,所以$t=\frac{d}{{v}_{0}}$;
该粒子恰好能够垂直于OL进入匀强磁场,所以在Y方向上,速度关系有:v0sinθ=at=$\frac{qE}{m}t$,
所以,${v}_{0}sinθ=\frac{qEd}{m{v}_{0}}$,则有$E=\frac{m{{v}_{0}}^{2}sinθ}{qd}=\frac{m{{v}_{0}}^{2}sin45°}{qd}=\frac{\sqrt{2}m{{v}_{0}}^{2}}{2qd}$.
(2)根据(1)可知粒子在电场中运动的时间$t=\frac{d}{{v}_{0}}$;
粒子在磁场中只受洛伦兹力的作用,在洛伦兹力作用下做圆周运动,设圆周运动的周期为T
粒子能在OL与x轴所围区间内返回到虚线OL上,则粒子从M点出发到第二次经过OL在磁场中运动了半个圆周,所以,在磁场中运动时间为$\frac{1}{2}T$;
粒子在磁场运动,洛伦兹力作为向心力,所以有,$Bvq=m\frac{{v}^{2}}{R}$;
根据(1)可知,粒子恰好能够垂直于OL进入匀强磁场,速度v就是初速度v0在X方向上的分量,即$v={v}_{0}cosθ={v}_{0}cos45°=\frac{\sqrt{2}}{2}{v}_{0}$;
粒子在电场中运动,在Y方向上的位移$Y=\frac{1}{2}{v}_{0}sinθ•t=\frac{\sqrt{2}}{4}{v}_{0}t=\frac{\sqrt{2}}{4}d$,所以,粒子进入磁场的位置在OL上距离O点$l=dcosθ+Y=\frac{3\sqrt{2}}{4}d$;
根据几何关系,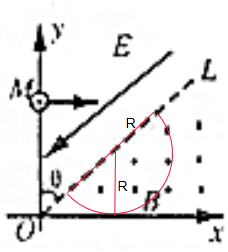
可得:$l≥R+\frac{R}{cosθ}$,即$R≤\frac{l}{1+\frac{1}{cosθ}}=\frac{\frac{3\sqrt{2}}{4}d}{1+\sqrt{2}}=\frac{3(2-\sqrt{2})}{4}d$;
所以,$T=\frac{2πR}{v}≤\frac{2π×\frac{3(2-\sqrt{2})}{4}d}{\frac{\sqrt{2}}{2}{v}_{0}}$=$\frac{3(\sqrt{2}-1)πd}{{v}_{0}}$;
所以,粒子从M点出发到第二次经过OL所需要的最长时间${t}_{最长}=t+\frac{1}{2}{T}_{max}$=$\frac{d}{{v}_{0}}+\frac{1}{2}\frac{3(\sqrt{2}-1)πd}{{v}_{0}}=\frac{d}{{v}_{0}}[1+\frac{3(\sqrt{2}-1)π}{2}]$.
答:(1)此电场的场强大小E为$\frac{\sqrt{2}m{{v}_{0}}^{2}}{2qd}$;
(2)若粒子能在OL与x轴所围区间内返回到虚线OL上,则粒子从M点出发到第二次经过OL所需要的最长时间为$\frac{d}{{v}_{0}}[1+\frac{3(\sqrt{2}-1)π}{2}]$.
点评 在求运动相关的问题时,要注意判断运动的方向,如本题中,在电场中运动,要注意在Y方向上是沿负方向即OL方向运动的,在磁场中一样需要判断粒子向哪边偏转,才能得到几何关系,若向上偏转的半圆则解出的结果R会比向下偏转得到的R大得多.


科目:高中物理 来源: 题型:选择题
| A. | 电子束通过双缝干涉实验装置后可以形成干涉图样,体现了电子等实物粒子也具有波动性 | |
| B. | 根据玻尔的原子结构理论,原子中电子绕核运动的轨道半径可以是任意值 | |
| C. | 只要光照时间足够长,任何金属都能发生光电效应 | |
| D. | ${\;}_{3}^{4}$H+${\;}_{1}^{2}$H→${\;}_{2}^{4}$He+${\;}_{0}^{1}$n是α衰变方程 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:计算题
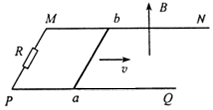 如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R的定值电阻.导体棒ab长l=0.5m,其电阻为r,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.
如图所示,水平面上有两根相距0.5m的足够长的平行金属导轨MN和PQ,它们的电阻可忽略不计,在M和P之间接有阻值为R的定值电阻.导体棒ab长l=0.5m,其电阻为r,与导轨接触良好.整个装置处于方向竖直向上的匀强磁场中,磁感应强度B=0.4T.现使ab以v=10m/s的速度向右做匀速运动.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 0.3m/s2 | B. | 0.35m/s2 | C. | 2.1m/s2 | D. | 4.2m/s2 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | m(v+v′)-mgt | B. | mgt | C. | $\frac{1}{2}$m(v-v′) | D. | 0 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 速度的改变量为$\frac{{v}_{0}}{2}$ | B. | 经历的时间为$\frac{\sqrt{3}m{v}_{0}}{2F}$ | ||
| C. | 发生的位移为$\frac{\sqrt{21}m{{v}_{0}}^{2}}{8F}$ | D. | 恒力F与v0的夹角为60° |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 100W | B. | 200W | C. | 300W | D. | 400W |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com