
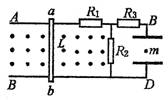
在竖直面内有两平行金属导轨AB、CD,间距为L,金属棒ab可在导轨上无摩擦地滑动。棒与导轨垂直,并接触良好.它们的电阻均可不计。导轨之间有垂直纸面向外的匀强磁场,磁感强度为B.导轨右边与电路连接。电路中的三个定值电照R1、R2、R3阻值分别为2R、R和0.5R。在BD间接有一水平放置的平行板电容器C,极板间距离为d.
(1)当ab以速度v0匀速向左运动时,电容器中质量为m的带电微粒恰好静止.试判断微粒的带电性质,及带电量的大小.
(2)当AB棒以某一速度沿导轨匀速运动时,发现带电微粒从两极板中间由静止开始向下运动,历时t=2×10-2 s到达下极板,已知电容器两极板间距离d=6×10-3m,求ab棒的速度大小和方向。(g=10m/s2)
(1) 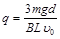 (2)
(2) 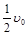
【解析】(1)棒匀速向左运动,感应电流为顺时针方向,电容器上板带正电.
∵微粒受力平衡,电场力向上,场强方向向下。 ∴微粒带负电。
设微粒带电量大小为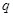 ,由平衡条件知:
,由平衡条件知:
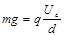 ①
①
对R1、R2和金属棒构成的回路,由欧姆定律可得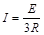 ②
②
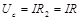 ③
③
由法拉第电磁感应定律可得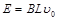 ④
④
由以上各式求得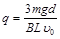 ⑤
⑤
(2)因带电微粒从极板中间开始向下作初速度为零的匀加速运动,
由运动学公式得: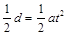 ⑥ [来源:学§科§网]
⑥ [来源:学§科§网]
得
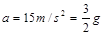 >
> ⑦
⑦
可见带电微粒受到的电场力向下,所以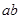 棒应向右运动,设此时极板间电压为
棒应向右运动,设此时极板间电压为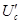 ,由牛顿第二定律,得
,由牛顿第二定律,得 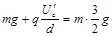 ⑧
⑧
出⑤和⑧得
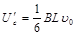
设棒ab运动速度为 ,则电动势
,则电动势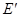 =
=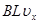 ,由欧姆定律得
,由欧姆定律得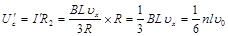
∴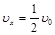 . 即棒运动速度大小应为原来速度的一半,即为
. 即棒运动速度大小应为原来速度的一半,即为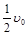 .
.


科目:高中物理 来源:2013届江西省高二下学期期中考试物理试卷(解析版) 题型:计算题
如图两根正对的平行金属直轨道MN、M´N´位于同一水平面上,两轨道间距L=0.50m.轨道
的MM′端之间接一阻值R=0.40Ω的定值电阻,NN′端与两条位于竖直面内的半圆形光滑金
属轨道NP、N′P′平滑连接,两半圆轨道的半径均为 R0 =0.50m.直轨道的右端处于竖直向下、
磁感应强度B =0.64T的匀强磁场中,磁场区域的宽度d=0.80m,且其右边界与NN′重合.现
有一质量 m =0.20kg、电阻 r =0.10Ω的导体杆ab静止在距磁场的左边界s=2.0m处.在与
杆垂直的水平恒力 F =2.0N的作用下ab杆开始运动,当运动至磁场的左边界时撤去F,结果导
体ab恰好能以最小速度通过半圆形轨道的最高点PP′.已知导体杆ab在运动过程中与轨道接
触良好,且始终与轨道垂直,导体杆ab与直轨道间的动摩擦因数 μ=0.10,轨道的电阻可忽略不
计,取g=10m/s2,求:

①导体杆穿过磁场的过程中通过电阻R上的电荷量
②导体杆穿过磁场的过程中整个电路产生的焦耳热
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com