
分析 (1)卫星绕行星做的是匀速圆周运动,结合轨道半径和周期求出卫星加速度;
(2)根据万有引力提供向心力,由牛顿第二定律求出行星的质量.再求行星的平均密度.
(3)根据行星表面万有引力提供向心力求解第一宇宙速度,即为此卫星的速度.
解答 解:(1)卫星绕行星做圆周运动,其加速度为:a=$\frac{4{π}^{2}}{{T}^{2}}{R}_{2}$
(2)根据万有引力提供向心力,由牛顿第二定律得:
G$\frac{Mm}{{R}_{2}^{2}}$=m$\frac{4{π}^{2}}{{T}^{2}}{R}_{2}$
可得行星的质量为:M=$\frac{4{π}^{2}{R}_{2}^{3}}{G{T}^{2}}$
因此该行星的平均密度为:ρ=$\frac{M}{V}$=$\frac{\frac{4{π}^{2}{R}_{2}^{3}}{G{T}^{2}}}{\frac{4}{3}π{R}_{1}^{3}}$=$\frac{3π{R}_{2}^{3}}{G{T}^{2}{R}_{1}^{3}}$
(3)靠近行星表面运行的人造卫星的轨道半径近似等于行星的半径R1.由万有引力提供向心力,得
G$\frac{Mm}{{R}_{1}^{2}}$=m$\frac{{v}^{2}}{{R}_{1}}$
联立解得:v=$\frac{2π{R}_{2}}{T}$$\sqrt{\frac{{R}_{2}}{{R}_{1}}}$
答:(1)该颗卫星加速度是$\frac{4{π}^{2}}{{T}^{2}}{R}_{2}$;
(2)该行星的平均密度是$\frac{3π{R}_{2}^{3}}{G{T}^{2}{R}_{1}^{3}}$;
(3)要在该星球上发射一颗靠近表面运行的人造卫星,此卫星的速度为$\frac{2π{R}_{2}}{T}$$\sqrt{\frac{{R}_{2}}{{R}_{1}}}$.
点评 解决本题的关键掌握卫星绕行星运行时,由万有引力提供向心力,运用万有引力定律和圆周运动的规律结合解答.


 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案科目:高中物理 来源: 题型:解答题
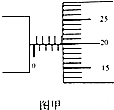 在“测定金属的电阻率”实验中,用螺旋测微器测量金属丝直径时的刻度位置如图甲所示,在测出金属丝的长度后,用伏安法测该金属丝的电阻R,(金属丝的电阻大约为5Ω).
在“测定金属的电阻率”实验中,用螺旋测微器测量金属丝直径时的刻度位置如图甲所示,在测出金属丝的长度后,用伏安法测该金属丝的电阻R,(金属丝的电阻大约为5Ω).
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
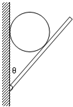
| A. | 墙壁受到的压力增大,木板受到的压力增大 | |
| B. | 墙壁受到的压力增大,木板受到的压力减小 | |
| C. | 墙壁受到的压力减小,木板受到的压力减小 | |
| D. | 墙壁受到的压力减小,木板受到的压力增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 一直增大 | B. | 一直减小 | C. | 先增大后减小 | D. | 先减小后增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 初速度为零的匀加速直线运动 | B. | 初速度不为零的匀加速直线运动 | ||
| C. | 匀速直线运动 | D. | 变速直线运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
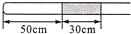 如图,一端封闭一端开口、内径均匀、长度为100cm的直玻璃管水平放置,管内有一段长为30cm的水银柱,平衡时封闭端空气柱长为50cm.若将管缓慢转动90°至开口端竖直向下,求稳定时封闭端空气柱的长度.设大气压强为75cmHg.整个过程温度保持不变.
如图,一端封闭一端开口、内径均匀、长度为100cm的直玻璃管水平放置,管内有一段长为30cm的水银柱,平衡时封闭端空气柱长为50cm.若将管缓慢转动90°至开口端竖直向下,求稳定时封闭端空气柱的长度.设大气压强为75cmHg.整个过程温度保持不变.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
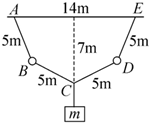 如图所示,AB、BC、CD和DE为质量可忽略的等长细线,长度均为5m,A、E端悬挂在水平天花板上,AE=14m,B、D是质量均相同的小球.质量为18千克的重物挂于C点,平衡时C点离天花板的垂直距离为7m,试求小球B、D的质量.
如图所示,AB、BC、CD和DE为质量可忽略的等长细线,长度均为5m,A、E端悬挂在水平天花板上,AE=14m,B、D是质量均相同的小球.质量为18千克的重物挂于C点,平衡时C点离天花板的垂直距离为7m,试求小球B、D的质量.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,宽阔的水平地面上固定一竖直高度为1m的薄木板,在与薄木板水平距离1m、距地面高度为1.8m处水平抛出一视为质点的玩具小鸟.不计空气阻力,g=10m/s2.则下列说法中正确的是( )
如图所示,宽阔的水平地面上固定一竖直高度为1m的薄木板,在与薄木板水平距离1m、距地面高度为1.8m处水平抛出一视为质点的玩具小鸟.不计空气阻力,g=10m/s2.则下列说法中正确的是( )| A. | 若水平初速度v0=10m/s,则玩具小鸟做平抛运动的时间是0.6s | |
| B. | 若水平初速度v0=10m/s,则玩具小鸟做平抛运动的时间是0.4s | |
| C. | 若任意改变水平初速度,则玩具小鸟击中木板时的速度的最小值为2$\sqrt{5}$m/s | |
| D. | 若任意改变水平初速度,则玩具小鸟击中木板时的速度的最小值为$\sqrt{5}$m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 某同学设计了一个测定列车加速度的仪器,如图所示,图中AB是一段半径为r 的四分之一圆弧形的合金轨道(其电阻不可忽略,横截粗细均匀),其A点切线竖直、B点切线水平,O为圆心;用长为r、电阻不计的柔软金属导线线将一个可视为质点的金属球悬挂在O点,金属球恰好与轨道良好接触且无摩擦.A、B之间接有内阻不计、电动势为9V的电池,并串入了一个理想电流表
某同学设计了一个测定列车加速度的仪器,如图所示,图中AB是一段半径为r 的四分之一圆弧形的合金轨道(其电阻不可忽略,横截粗细均匀),其A点切线竖直、B点切线水平,O为圆心;用长为r、电阻不计的柔软金属导线线将一个可视为质点的金属球悬挂在O点,金属球恰好与轨道良好接触且无摩擦.A、B之间接有内阻不计、电动势为9V的电池,并串入了一个理想电流表 ,O、B间还接有一个理想电压表
,O、B间还接有一个理想电压表 ,整个装置安装在与列车前进的方向平行的竖直平面内.下列说法中正确的是( )
,整个装置安装在与列车前进的方向平行的竖直平面内.下列说法中正确的是( )| A. | 从图中看到列车一定是向右加速运动 | |
| B. | 当列车的加速度增大时,电压表 的读数减小 的读数减小 | |
| C. | 当列车的加速度增大时,电流表 的读数增大 的读数增大 | |
| D. | 若电压表显示3 V,则列车的加速度为$\frac{\sqrt{3}}{3}$g |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com