

分析 (1)物体A、B第一次碰撞时,当速度相同时,弹簧压缩的最短,弹性势能最大,根据动量守恒定律和能量守恒定律列式后联立求解即可;
(2)M远远大于m,经过n次碰撞后,两物体速度近似相等,弹簧l对物块A的总冲量达到最大值,根据动量定理和能量守恒定律列式求解;
(3)第一次碰撞过程,根据动量守恒定律和能量守恒定律列式求解末速度;第二次碰撞过程同样根据动量守恒定律和能量守恒定律列式求解末速度;通过计算会发现第二次碰撞后B的速度开始小于A的速度.
解答 解:(1)物体A、B第一次碰撞时,当速度相同时,弹簧压缩的最短,弹性势能最大;
对B滑块,根据能量守恒定律,有:
E=$\frac{1}{2}m{v}^{2}$
根据动量守恒定律,有:
mv=(M+m)v′
根据能量守恒定律,有:
E=$\frac{1}{2}(M+m){v}^{2}+{E}_{p}$
联立解得:
Ep=$\frac{M}{M+m}E$
(2)M远远大于m,经过多次碰撞后,两个物体速度相同,根据能量守恒定律,有:
E=$\frac{1}{2}(M+m){{v}_{1}}^{2}$
由于M>>m,故:
${v}_{1}=\sqrt{\frac{2E}{M+m}}$
根据动量定理,弹簧l对物块A的总冲量的最大值为:
I=Mv1=M$\sqrt{\frac{2E}{M+m}}$;
(3)已知M=5m,B与A碰撞前,有:
E=$\frac{1}{2}m{v}^{2}$
物体A、B第一次碰撞后,根据动量守恒定律和能量守恒定律,有:
mv=Mv1+mv2
E=$\frac{1}{2}M{v}_{1}^{2}+\frac{1}{2}m{v}_{2}^{2}$
其中:M=5m
联立解得:
${v}_{1}=\frac{1}{3}v$=$\frac{1}{3}\sqrt{\frac{2E}{m}}$
v2=-$\frac{2}{3}v$=-$\frac{2}{3}\sqrt{\frac{2E}{m}}$
(另一组解是碰撞后两个球的速度均不变,不合实际,舍去)
物体A、B第一次碰撞后,根据动量守恒定律和能量守恒定律,有:
Mv1-mv2=Mv3+mv4
E=$\frac{1}{2}M{v}_{3}^{2}+\frac{1}{2}m{v}_{4}^{2}$
联立解得:
v3=$\frac{4}{9}v$=$\frac{4}{9}$$\sqrt{\frac{2E}{m}}$
${v}_{4}=-\frac{1}{9}v$=-$\frac{1}{9}$$\sqrt{\frac{2E}{m}}$
(另一组解是碰撞后两个球的速度均不变,不合实际,舍去)
故此后B反弹后不会在追上A;
答:(1)弹簧l所能获得的最大弹性势能为$\frac{M}{M+m}E$;
(2)若已知M远远大于m,求整个运动过程中弹簧l对物块A的总冲量的最大值为M$\sqrt{\frac{2E}{M+m}}$;
(3)若已知M=5m,A、B最后的运动速度分别为$\frac{4}{9}$$\sqrt{\frac{2E}{m}}$、$\frac{1}{9}$$\sqrt{\frac{2E}{m}}$.
点评 本题是动量与能量综合的问题,关键是明确碰撞过程中系统的动量守恒,同时结合机械能守恒定律列式分析;第三问要对每次碰撞过程讨论,直到不能碰撞为止.


科目:高中物理 来源: 题型:多选题
| A. | 库仑定律适用于真空中两个点电荷之间的相互作用力 | |
| B. | 两个带电小球即使相距非常近,也能用库仑定律 | |
| C. | 相互作用的两个点电荷,不论它们的电荷量是否相同,它们之间的库仑力大小一定相等 | |
| D. | 两个点电荷的电量各减为原来的一半,它们之间的距离保持不变,则它们之间库存仑力减为原来的一半 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
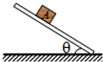 如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )
如图所示,质量为1kg的物块A放在与水平面成θ的倾斜木板上,当θ=30°时物块恰好处于平衡状态.已知物块A距离木板下端的距离为$\sqrt{3}$v0,E=10m/s2,滑动摩擦力与最大静摩擦力相等,则以下分析正确的是( )| A. | 物块与木板之间的摩擦因数μ=$\frac{\sqrt{3}}{3}$ | |
| B. | 将木块与水平面的视角改为60°,再释放物块,其运动加速度为$\frac{10\sqrt{3}}{3}$m/s2 | |
| C. | 将木板与水平面的倾角改为60°,再释放物块,其运动到木板下端的速度为2$\sqrt{3}$m/s | |
| D. | 将木板与水平桌面的倾角改为60°,再释放物块,其运动到木板下端的过程中重力做功5$\sqrt{3}$J |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 位移是5m | B. | 路程是5m | C. | 位移大小是3m | D. | 以上均不对 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
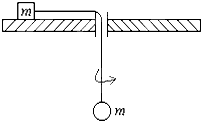 如图所示,质量为m的木块,用光滑细绳拴着,置于很大的水平转盘上,细绳穿过转盘中央的光滑细管,与质量也为m的小球相连,木块的最大静摩擦力为其重力的μ倍(μ=0.2),当转盘以角速度ω=4弧度/秒匀速转动时,要保持木块与转盘相对静止,木块转动的轨道半径的范围是多少?(g=10m/s2,结果保留两位有效数字)
如图所示,质量为m的木块,用光滑细绳拴着,置于很大的水平转盘上,细绳穿过转盘中央的光滑细管,与质量也为m的小球相连,木块的最大静摩擦力为其重力的μ倍(μ=0.2),当转盘以角速度ω=4弧度/秒匀速转动时,要保持木块与转盘相对静止,木块转动的轨道半径的范围是多少?(g=10m/s2,结果保留两位有效数字)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,木块从左边斜面的A点自静止开始下滑,经过一段水平面后,又滑上右边斜面并停留在B点.若动摩擦因数处处相等,AB连线与水平面夹角为θ,不考虑木块在路径转折处碰撞损失的能量,则( )
如图所示,木块从左边斜面的A点自静止开始下滑,经过一段水平面后,又滑上右边斜面并停留在B点.若动摩擦因数处处相等,AB连线与水平面夹角为θ,不考虑木块在路径转折处碰撞损失的能量,则( )| A. | 木块与接触面间的动摩擦因数为sinθ | |
| B. | 木块与接触面间的动摩擦因数为tanθ | |
| C. | 两斜面的倾角一定大于θ | |
| D. | 右边斜面的倾角可以大于θ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com