
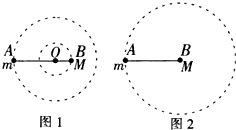
 如图1所示,质量分别为m和M的两个星球A和B在相互作用的引力作用下都绕O点做勻速圆周运动,运动的周期均为T1;如果是星球A围绕星球B做勻速圆周运动且保持星球A与B间的距离不变,如图2所示,运动的周期为T2,则T1与T2之比为( )
如图1所示,质量分别为m和M的两个星球A和B在相互作用的引力作用下都绕O点做勻速圆周运动,运动的周期均为T1;如果是星球A围绕星球B做勻速圆周运动且保持星球A与B间的距离不变,如图2所示,运动的周期为T2,则T1与T2之比为( )| A. | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{M+m}{M}}$ | B. | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{M}{M+m}}$ | C. | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{M+m}{m}}$ | D. | $\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{m}{M+m}}$ |
分析 图1是双星问题,A和B绕O做匀速圆周运动,它们之间的万有引力提供各自的向心力,A和B有相同的角速度和周期,结合牛顿第二定律和万有引力定律列式求解周期;图2中万有引力提供向心力,根据牛顿第二定律列式求解周期即可.
解答 解:对于图1,设两个星球A和B做匀速圆周运动的轨道半径分别为r和R,两个星球间距为L,相互作用的万有引力大小为F,运行周期为T1.
根据万有引力定律有:
F=G$\frac{Mm}{(R+r)^{2}}$ ①
由匀速圆周运动的规律得:
F=m($\frac{2π}{{T}_{1}}$)2r ②
F=M($\frac{2π}{{T}_{1}}$)2R ③
由题意有:L=R+r ④
联立①②③④式得:
T1=2π$\sqrt{\frac{{L}^{3}}{G(M+m)}}$
对于图2,万有引力等于向心力,故:
$G\frac{Mm}{{L}^{2}}=m\frac{4{π}^{2}}{{T}_{2}^{2}}L$
解得:
${T}_{2}=2π\sqrt{\frac{{L}^{3}}{GM}}$
故$\frac{{T}_{1}}{{T}_{2}}$=$\sqrt{\frac{M}{M+m}}$
故选:B.
点评 本题关键是建立天体的运动模型;对于双星问题,关键我们要抓住它的特点,即两星球的万有引力提供各自的向心力和两星球具有共同的周期;当M>>m时,题中两个模型是等价的.


科目:高中物理 来源: 题型:解答题
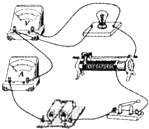 “描绘小灯泡的伏安特性曲线”实验要求小灯泡两端的电压能从O到额定电压之问连续调节.某同学连接的实物电路如图.
“描绘小灯泡的伏安特性曲线”实验要求小灯泡两端的电压能从O到额定电压之问连续调节.某同学连接的实物电路如图.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,水平地面上有一楔形物块a,其斜面上有一小物体b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上,a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动,当它们刚运行至轨道的粗糙段时( )
如图,水平地面上有一楔形物块a,其斜面上有一小物体b,b与平行于斜面的细绳的一端相连,细绳的另一端固定在斜面上,a与b之间光滑,a和b以共同速度在地面轨道的光滑段向左运动,当它们刚运行至轨道的粗糙段时( )| A. | 绳的拉力减小,b对a的压力减小 | |
| B. | 绳的拉力增加,斜面对b的支持力增加 | |
| C. | 绳的拉力减小,地面对a的支持力增加 | |
| D. | 绳的拉力增加,地面对a的支持力减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 81:80 | B. | 80:81 | C. | 9:1 | D. | 1:9 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 物体的动量不断增大 | |
| B. | 物体的动量先增大后减小 | |
| C. | 变化的力减小到零时物体的动量最大 | |
| D. | 两力恢复到再次平衡时物体的动量最大 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图,第一象限内存在沿y轴负方向的匀强电场,电场强度大小为E,第二,三,四象限存在方向垂直xOy平面向外的匀强磁场,其中第二象限的磁感应强度大小为B,第三,四象限磁感应强度大小相等,一带正电的粒子,从P(-d,0)点沿与x轴正方向成α=60°角平行xOy平面入射,经第二象限后恰好由y轴上的Q点(图中未画出)垂直y轴进入第一象限,之后经第四,三象限重新回到P点,回到P点时速度方向与入射时相同,不计粒子重力,求:
如图,第一象限内存在沿y轴负方向的匀强电场,电场强度大小为E,第二,三,四象限存在方向垂直xOy平面向外的匀强磁场,其中第二象限的磁感应强度大小为B,第三,四象限磁感应强度大小相等,一带正电的粒子,从P(-d,0)点沿与x轴正方向成α=60°角平行xOy平面入射,经第二象限后恰好由y轴上的Q点(图中未画出)垂直y轴进入第一象限,之后经第四,三象限重新回到P点,回到P点时速度方向与入射时相同,不计粒子重力,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
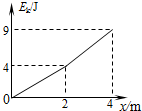 质量m=2kg的物块放在粗糙水平面上,在水平拉力的作用下由静止开始运动,物块动能Ek与其发生位移x之间的关系如图所示.已知物块与水平面间的动摩擦因数μ=0.2,则下列说法中正确的是( )
质量m=2kg的物块放在粗糙水平面上,在水平拉力的作用下由静止开始运动,物块动能Ek与其发生位移x之间的关系如图所示.已知物块与水平面间的动摩擦因数μ=0.2,则下列说法中正确的是( )| A. | x=1m时物块的速度大小为2m/s | |
| B. | x=3m时物块的加速度大小为1.25m/s2 | |
| C. | 在前2m位移的运动过程中物块所经历的时间为2s | |
| D. | 在前4m位移的运动过程中拉力对物块做的功为25J |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com