
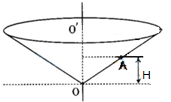
 如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )
如图所示,一个竖直放置的圆锥筒可绕其中心轴OO′匀速转动,筒口半径和筒高之比为4:3,筒内壁粗糙、内壁上有一质量为m的小物块A,与内壁之间的动摩擦因数为0.5,距筒底的高度为H,当圆筒转动时,以下角速度中,可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下的是( )| A. | $\sqrt{\frac{g}{2H}}$ | B. | $\sqrt{\frac{5g}{8H}}$ | C. | $\sqrt{\frac{3g}{2H}}$ | D. | $\sqrt{\frac{2g}{H}}$ |
分析 当物块在A点随筒做匀速转动,且其受到的摩擦力为零时,由重力和支持力的合力提供物块的向心力,由牛顿第二定律求解.
当角速度最大时筒壁对物块的最大静摩擦力沿筒壁向下,由牛顿第二定律列式求解.
解答 解:由于筒口半径和筒高之比为4:3,有几何关系可知,筒内壁与竖直方向之间的夹角θ满足:
tanθ=$\frac{r}{h}=\frac{4}{3}$
所以:θ=53°
当物块在A点随筒做匀速转动,且其受到的摩擦力为零时,由重力和支持力的合力提供物块水平方向的向心力,由牛顿第二定律得:
mgtanθ=mω2r
其中:r=Htanθ
可得:ω=$\sqrt{\frac{g}{H}}$
当角速度最大时筒壁对物块的最大静摩擦力沿筒壁向下,由牛顿第二定律,
竖直方向有:Ncosθ=fsinθ+mg
水平方向有:Nsinθ+fcosθ=mωm2r
又 f=μN
联立得:ωm=$\sqrt{\frac{3g}{2H}}$
最大角速度不能超过$\sqrt{\frac{3g}{2H}}$.
所以:可以使物体与圆筒间有静摩擦力且静摩擦力方向沿简壁向下时:$\sqrt{\frac{g}{H}}$<ω≤$\sqrt{\frac{3g}{2H}}$
只有C选项符合题意.
故选:C
点评 本题是圆锥摆类型.关于向心力应用的基本方程是:指向圆心的合力等于向心力,其实是牛顿第二定律的特例.


 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案 口算心算速算应用题系列答案
口算心算速算应用题系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 长L=0.5m、质量可忽略的杆,其一端固定于O点,另一端连有质量m=2kg的小球,它绕O点在竖直平面内做圆周运动,当通过最高点时,如图所示.g=10m/s2,求:
长L=0.5m、质量可忽略的杆,其一端固定于O点,另一端连有质量m=2kg的小球,它绕O点在竖直平面内做圆周运动,当通过最高点时,如图所示.g=10m/s2,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
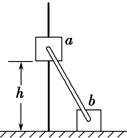 如图,滑块a、b的质量均为m=1kg,a套在固定竖直杆上,与光滑水平地面相距h=0.2m,b放在地面上.a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点.
如图,滑块a、b的质量均为m=1kg,a套在固定竖直杆上,与光滑水平地面相距h=0.2m,b放在地面上.a、b通过铰链用刚性轻杆连接,由静止开始运动.不计摩擦,a、b可视为质点.查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
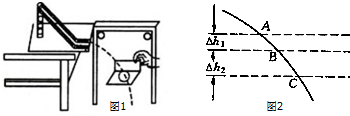
 一个质点A在光滑的水平面上运动,它受到另一个固定质点B的排斥力的作用,已知质点A的轨迹如图中的曲线所示,图中P、Q两点为轨迹上的点,虚线是过P、Q两点并与轨迹相切的中线,两虚线和轨迹平面分成四个区域,判断质点B的可能位置,下列说法中正确的是( )
一个质点A在光滑的水平面上运动,它受到另一个固定质点B的排斥力的作用,已知质点A的轨迹如图中的曲线所示,图中P、Q两点为轨迹上的点,虚线是过P、Q两点并与轨迹相切的中线,两虚线和轨迹平面分成四个区域,判断质点B的可能位置,下列说法中正确的是( )| A. | 可能在④区域,而不可能在①②③区域 | B. | 可能在①区域,而不可能在②③④区域 | ||
| C. | 可能在①②区域,而不可能在③④区域 | D. | 可能在①②④区域,而不可能在③区域 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
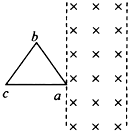 如图所示,abc为边长为L的正三角形线框,匀强磁场与线框平面垂直,其宽度为L.现线框从图位置以恒定的速度通过场区,线框中的感应电流随时间的变化图象正确的是(逆时针为电流的正方向)( )
如图所示,abc为边长为L的正三角形线框,匀强磁场与线框平面垂直,其宽度为L.现线框从图位置以恒定的速度通过场区,线框中的感应电流随时间的变化图象正确的是(逆时针为电流的正方向)( )| A. |  | B. |  | C. | 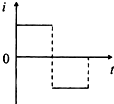 | D. | 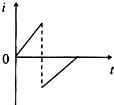 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 人匀速前进,则车匀速后退 | |
| B. | 人匀加速前进,车匀加速后退,两者对地加速度大小相等 | |
| C. | 不管人如何走,任意时刻人和车动量大小总相等 | |
| D. | 人停止走动,车也静止 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com