
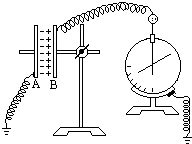
| A. | 将两极板的间距加大 | |
| B. | 将两极板平行错开,使正对面积减小 | |
| C. | 在A板的内表面上放置一面积和极板相等、厚度小于极板间距的陶瓷板 | |
| D. | 在A板的内表面上放置一面积和极板相等、厚度小于极板间距的铝板 |
分析 解答本题关键掌握:静电计测定电容器板间的电势差,电势差越大,指针偏角越大;
电容器电容的决定式C=$\frac{?S}{4πkd}$,分析电容的变化;
电容器的电量不变,由电容器的定义式$C=\frac{Q}{U}$分析电势差的变化.
解答 解:
A、将两极板的间距加大,依据$C=\frac{?S}{4πkd}$可知电容减小,由电容器的定义式$C=\frac{Q}{U}$,可知两极板间电压增大,故指针偏角增大,故A错误.
B、将两极板平行错开,使正对面积减小,依据$C=\frac{?S}{4πkd}$可知电容减小,由电容器的定义式$C=\frac{Q}{U}$,可知两极板间电压增大,故指针偏角增大,故B错误.
CD、在A板的内表面上放置一面积和极板相等、厚度小于极板间距的陶瓷板或铝板,都是增大了介电常数,依据$C=\frac{?S}{4πkd}$可知电容增大,由电容器的定义式$C=\frac{Q}{U}$,可知两极板间电压减小,故指针偏角减小,故C正确,D正确.
故选:CD.
点评 对于电容器动态变化分析问题,关键根据电容的决定式$C=\frac{?S}{4πkd}$和定义式$C=\frac{Q}{U}$结合进行分析,同时要抓住不变量,一般电容器动态问题都能解决.


 一线名师提优试卷系列答案
一线名师提优试卷系列答案 阳光试卷单元测试卷系列答案
阳光试卷单元测试卷系列答案科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 曲线运动一定是变速运动 | |
| B. | 曲线运动中加速度一定不为零,但可以等于恒量 | |
| C. | 做匀速圆周运动的物体处于平衡状态 | |
| D. | 匀速圆周运动的线速度方向始终与半径垂直 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
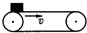 如图所示,质量为m的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v匀速运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从静止释放到相对传送带静止这一过程下列说法正确的是( )
如图所示,质量为m的物体在水平传送带上由静止释放,传送带由电动机带动,始终保持以速度v匀速运动,物体与传送带间的动摩擦因数为μ,物体过一会儿能保持与传送带相对静止,对于物体从静止释放到相对传送带静止这一过程下列说法正确的是( )| A. | 电动机多做的功为$\frac{1}{2}$mv2 | B. | 摩擦力对物体做的功为$\frac{1}{2}$mv2 | ||
| C. | 电动机增加的功率为μmgv | D. | 传送带克服摩擦力做功为$\frac{1}{2}$mv2 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
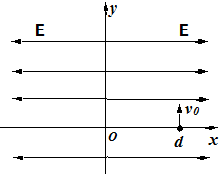 如图所示,在x>0的空间中,存在沿x轴方向的匀强电场E;在x<0的空间中,存在沿x轴负方向的匀强电场,场强大小也为E.一电子(-e,m)在x=d处的P点以沿y轴正方向的初速度v0开始运动,不计电子重力.求:
如图所示,在x>0的空间中,存在沿x轴方向的匀强电场E;在x<0的空间中,存在沿x轴负方向的匀强电场,场强大小也为E.一电子(-e,m)在x=d处的P点以沿y轴正方向的初速度v0开始运动,不计电子重力.求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
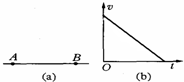 如图(a)所示,AB是某电场中的一条电场线.若有一电子以某一初速度并且仅在电场力的作用下,沿AB由点A运动到点B,其速度图象如图(b)所示.下列关于A、B两点的电势ϕ和电场强度E大小的判断正确的是( )
如图(a)所示,AB是某电场中的一条电场线.若有一电子以某一初速度并且仅在电场力的作用下,沿AB由点A运动到点B,其速度图象如图(b)所示.下列关于A、B两点的电势ϕ和电场强度E大小的判断正确的是( )| A. | EA>EB | B. | EA=EB | C. | ϕA>ϕB | D. | ϕA<ϕB |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
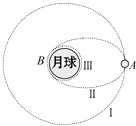 “神舟”七号飞船的成功发射为我国在2010年实现探月计划--“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0,飞船在距月球表面高度为3R的圆形轨道Ⅰ运行,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,万有引力常量为G,求:
“神舟”七号飞船的成功发射为我国在2010年实现探月计划--“嫦娥工程”获得了宝贵的经验.假设月球半径为R,月球表面的重力加速度为g0,飞船在距月球表面高度为3R的圆形轨道Ⅰ运行,到达轨道的A点时点火变轨进入椭圆轨道Ⅱ,到达轨道的近月点B再次点火进入月球近月轨道Ⅲ绕月球做圆周运动,万有引力常量为G,求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com