
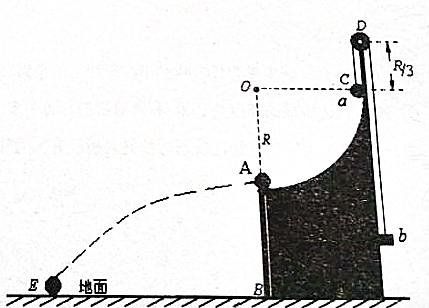
���� ��1����С����CA֮���˶��Ĺ�����ֻ�������������ɻ�е���غ㶨�ɼ������С��Aʱ���ٶȣ�Ȼ����ƽ���˶����ص㼴���������ĸ߶ȣ�
��С����CA֮����˶������ڵ��ڣ������ɵ��ڵ����ڹ�ʽ���ʱ�䣻С����ƽ���˶���ʱ����߶�h�йأ������Ƚϼ��ɣ�
��2��������������ӣ���С��a��C���Ӿ�ֹ��ʼ��֧�ܻ��£����˶��Ĺ�����a��b��ɵ�ϵͳ�����е���غ㣬��С��a��A����ٶȷֽ⣬���a��B���ٶȹ�ϵ��Ȼ���϶��ܶ���������������
��� �⣺��1���ټ���DC���������a��C��A�Ĺ����л�е���غ㣬��$\frac{1}{2}•2m{v}_{1}^{2}=2m•gR$
�ã�${v}_{1}=\sqrt{2gR}$
С���뿪�������ƽ���˶�ˮƽ����2R=v1•t2
���ԣ�${t}_{2}=\frac{2R}{{v}_{1}}=\frac{2R}{\sqrt{2gR}}=\sqrt{\frac{2R}{g}}$
������ĸ߶ȣ�h=$\frac{1}{2}g{t}_{2}^{2}=\frac{1}{2}g��\frac{2R}{g}=R$
��С����CA֮����˶������ڵ����˶�����C����ʱ����$\frac{1}{4}T$�����ԣ�
${t}_{1}=\frac{1}{4}•2��\sqrt{\frac{R}{g}}=\frac{��}{2}•\sqrt{\frac{R}{g}}��{t}_{2}=\sqrt{\frac{2R}{g}}$
��2��������������ӣ���С��a��C���Ӿ�ֹ��ʼ��֧�ܻ��µĹ�����b�����˶������ڲ���һ��Ħ������a��b��ɵ�ϵͳ�Ļ�е���غ㣮
��С��a��A����ٶ������ӵķ���ʹ�ֱ�����ӵķ���ֽ⣬��ͼ���������ӷ���ķ��ٶ���С��b���ٶȵĴ�С����ȵģ���
��ͼ�м��ι�ϵ��֪��$tan��=\frac{R+\frac{R}{3}}{R}=\frac{4}{3}$��$\frac{R}{\overline{AD}}=cos��$
���ԣ���=53�㣬$\overline{AD}=\frac{5R}{3}$
��ͼ�м��ι�ϵ��vacos��=vb
���ԣ�vb=0.6va
��С��a��C���Ӿ�ֹ��֧�ܻ��µĹ�����a��b��ɵ�ϵͳ�����е���غ�ã�
2m•gR-mg��$\overline{AD}-\frac{R}{3}$��=$\frac{1}{2}•2m{v}_{a}^{2}+\frac{1}{2}m{v}_{b}^{2}$
�������Ϸ��̵ã�${v}_{a}=0.75\sqrt{gR}$
С��a��C��A�Ĺ������ܵ�������֧���������ӵ�������֧�������������ɶ��ܶ����ã�
$2mgR+{W}_{����}=\frac{1}{2}•2m{v}_{a}^{2}-0$
���ԣ�${W}_{����}=-\frac{25}{16}mgR$
�𣺣�1���ٲ��С�����E�������ӵ�ˮƽ����EB����2R������AB�ĸ߶���R��
����С��a��C����A����ʱ��t1����A�˶���E��ʱ��Ϊt2����t1��t2��
��2��������������ӣ���С��a��C���Ӿ�ֹ��ʼ��֧�ܻ��£���C��A����������������a�������Ĺ���$-\frac{25}{16}mgR$��
���� �����е�����ʵ�ʶ�Ӧ�������ֲ�ͬ���������һ�ֵ�����Ƚϼ����ڶ��ֵ�����£�С��a��С��b���ٶȴ�С�Dz���ȵģ���Ҫ��a���ٶȷֽ�����ʹ�ö��ܶ������е���غ㶨�ɣ�������Ŀ���ѵ㣬Ҳ�Ƿdz����׳����ĵط���Ҫ�ر�ע�⣮


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ��2016-2017ѧ�꼪�ֳ��������ѧУ�߶������п������Ծ��������棩 ���ͣ�ѡ����
��ͼ��ʾ������A��B���ֱ��������磬�����ֱ�Ϊ4Q��Q����AB�����ϣ��糡ǿ��Ϊ��ĵط��ڣ� ��
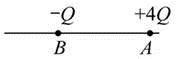
A. A��B֮��
B. A�Ҳ�
C. B���
D. A���Ҳ༰B�����
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ʹ�������� | B�� | ʹ��ѹ���� | ||
| C�� | ʹ��¯�ĵ������ | D�� | ʹ��ѹ�͵�¯�ĵ������һ�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����е����ڱȵ�����ת�����ڴ� | |
| B�� | �����еĽ��ٶȱȵ�����ת�Ľ��ٶȴ� | |
| C�� | �������ڱ������Ϸ��������ҹ��������������е���ת�� | |
| D�� | �����еĹ��ƽ��һ������ƽ���غ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
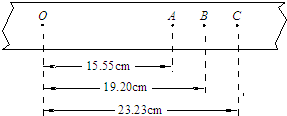
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | �����˶����ٶ�Ϊ$\sqrt{2Rg}$ | B�� | �����˶�������Ϊ4��$\sqrt{\frac{2R}{g}}$ | ||
| C�� | �����˶��ļ��ٶ�Ϊ$\frac{1}{2}$g | D�� | ���ǵĽ��ٶ�Ϊ$\frac{1}{4}$mRg |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
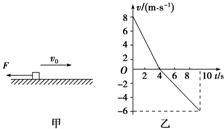 ����Ϊm=2kg��������ˮƽ��������ֱ���˶���t=0ʱ���ܵ�һ��ˮƽ����ĺ���F����ͼ����ʾ���˺������v-tͼ����ͼ����ʾ��ȡˮƽ����Ϊ������g=10m/s2��������
����Ϊm=2kg��������ˮƽ��������ֱ���˶���t=0ʱ���ܵ�һ��ˮƽ����ĺ���F����ͼ����ʾ���˺������v-tͼ����ͼ����ʾ��ȡˮƽ����Ϊ������g=10m/s2��������| A�� | ������ˮƽ���Ķ�Ħ������Ϊ��=0.5 | |
| B�� | 10sĩ����F��˲ʱ����Ϊ6W | |
| C�� | 10sĩ�����ڼ�ʱ������2m�� | |
| D�� | 10s������˷�Ħ��������34J |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com