
| A. | 两星间的万有引力不变 | B. | 白矮星的轨道半径不变 | ||
| C. | 类日伴星的运动速率减小 | D. | 两星的运动周期保持不变 |
分析 根据万有引力提供向心力,抓住向心力大小相等,以及周期相等,得出周期的表达式,从而分析其是否变大,抓住向心力相等得出轨道半径和质量的关系,从而分析轨道半径的变化.
解答 解:A、两星间距离在一段时间内不变,由万有引力定律可知,两星的质量总和不变而两星质量的乘积必定变化,则万有引力必定变化.故A错误.
B、由$G\frac{{M}_{1}{M}_{2}}{{L}^{2}}={M}_{1}{R}_{1}\frac{4{π}^{2}}{{T}^{2}}$=${M}_{2}{R}_{2}\frac{4{π}^{2}}{{T}^{2}}$,M1R1=M2R2.知双星运行半径与质量成反比,类日伴星的质量逐渐减小,故其轨道半径增大.故B错误.
C、组成的双星系统的周期T相同,设白矮星与类日伴星的质量分别为M1和M2,圆周运动的半径分别为R1和R2,由万有引力定律提供向心力:$G\frac{{M}_{1}{M}_{2}}{{L}^{2}}={M}_{1}{R}_{1}\frac{4{π}^{2}}{{T}^{2}}$=${M}_{2}{R}_{2}\frac{4{π}^{2}}{{T}^{2}}$,可得:GM1=$\frac{4{π}^{2}{R}_{2}{L}^{2}}{{T}^{2}}$,$G{M}_{2}=\frac{4{π}^{2}{R}_{1}{L}^{2}}{{T}^{2}}$,两式相加G(M1+M2)T2=4π2L3,白矮星与类日伴星的总质量不变,则周期T不变.由于类日伴星的轨道半径变大,根据v=$\frac{2πr}{T}$知,类日伴星的运动速率变大,故C错误,D正确.
故选:D.
点评 解决本题的关键知道组成的双星系统的周期T相同,抓住向心力大小相等,结合牛顿第二定律进行求解,难度中等.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:解答题
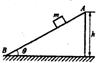 如图所示,质量m=1kg的小滑块,由静止从倾角θ=37°的固定粗糙斜面顶端A滑至底端B,已知滑块与斜面间的动摩擦因数为μ=0.5,A点距离水平地面的高度为h=0.6m,(g=10m/s2),求:
如图所示,质量m=1kg的小滑块,由静止从倾角θ=37°的固定粗糙斜面顶端A滑至底端B,已知滑块与斜面间的动摩擦因数为μ=0.5,A点距离水平地面的高度为h=0.6m,(g=10m/s2),求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 为了测量滑块与木板之间的动摩擦因数,采用如图所示装置:表面粗糙的木板固定在水平桌面上,左端装有定滑轮;木板上有一滑块,一端通过跨过定滑轮的细线与托盘连接,另一端与穿过打点计时器的纸带相连.实验中保持木板水平且细线平行于木板,在托盘中放入适量砝码后,滑块做匀加速直线运动,纸带上打出一系列的点.利用纸带测得滑块加速度为a,并已知重力加速度为g.
为了测量滑块与木板之间的动摩擦因数,采用如图所示装置:表面粗糙的木板固定在水平桌面上,左端装有定滑轮;木板上有一滑块,一端通过跨过定滑轮的细线与托盘连接,另一端与穿过打点计时器的纸带相连.实验中保持木板水平且细线平行于木板,在托盘中放入适量砝码后,滑块做匀加速直线运动,纸带上打出一系列的点.利用纸带测得滑块加速度为a,并已知重力加速度为g.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
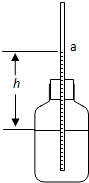 如图,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内水面有一定的高度差.已知地面附近高度每升高12m,大气压降低1mmHg;水银的密度为13.6×103kg/m3.
如图,在一个密闭的玻璃瓶的塞子上插入一根两端开口且足够长的细玻璃管,瓶内有一定量的水和空气.由于内外压强差,细玻璃管内水面a将与瓶内水面有一定的高度差.已知地面附近高度每升高12m,大气压降低1mmHg;水银的密度为13.6×103kg/m3.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 2016年我国将发射“天宫二号”空间实验室,并发射货运飞船与“天宫二号”交会对接.如图所示,飞船与“天宫二号”空间实验室交会对接前,假设运动中受到空气阻力,“天宫二号”从圆轨道Ⅰ变轨至圆轨道Ⅱ,已知地球半径为R,轨道I距地面高度为h1,轨道Ⅱ距地面高度为h2,“天宫二号”质量为m,则关于“天宫二号”的变轨过程,下列说法正确的是( )
2016年我国将发射“天宫二号”空间实验室,并发射货运飞船与“天宫二号”交会对接.如图所示,飞船与“天宫二号”空间实验室交会对接前,假设运动中受到空气阻力,“天宫二号”从圆轨道Ⅰ变轨至圆轨道Ⅱ,已知地球半径为R,轨道I距地面高度为h1,轨道Ⅱ距地面高度为h2,“天宫二号”质量为m,则关于“天宫二号”的变轨过程,下列说法正确的是( )| A. | 变轨前后线速度大小的比值为$\sqrt{\frac{R+{h}_{1}}{R+{h}_{2}}}$ | |
| B. | 变轨前后周期的比值为$\sqrt{\frac{(R+{h}_{1})^{2}}{(R+{h}_{2})^{2}}}$ | |
| C. | 变轨前后向心加速度大小的比值为$\frac{(R+{h}_{1})^{2}}{(R+{h}_{2})^{2}}$ | |
| D. | 变轨过程中“天宫二号”引力势能的减小量大于动能的增加量 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 2:1 | B. | 1:2 | C. | 1:4 | D. | 4:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示为一自卸货车,在卸货时,车厢由水平位置缓慢抬起,车厢与水平面的倾角缓慢增大的过程中,刚开始车厢与货物相对静止,当倾角增大到某一角度时,货物相对车厢下滑,之后倾角继续缓慢增大.在车厢由水平位置缓慢抬起、倾角缓慢增大,货物离开车厢之前的整个过程中,下列说法正确的是( )
如图所示为一自卸货车,在卸货时,车厢由水平位置缓慢抬起,车厢与水平面的倾角缓慢增大的过程中,刚开始车厢与货物相对静止,当倾角增大到某一角度时,货物相对车厢下滑,之后倾角继续缓慢增大.在车厢由水平位置缓慢抬起、倾角缓慢增大,货物离开车厢之前的整个过程中,下列说法正确的是( )| A. | 车厢对货物的支持力始终减小 | B. | 车厢对货物的摩擦力先增大后减小 | ||
| C. | 车厢对货物的作用力始终不变 | D. | 车厢对货物的摩擦力先减小后增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 如图,吊灯A通过绳子悬挂在天花板上的B点和C点,OB与天花板的夹角为α,OB、OA的长均为l.若灯的大小和线的长度相比是很小的,则吊灯在垂直于纸面内作小幅振动时的悬点为点Oˊ(填写图中的字母),周期为$2π\sqrt{\frac{l+lsinα}{g}}$.
如图,吊灯A通过绳子悬挂在天花板上的B点和C点,OB与天花板的夹角为α,OB、OA的长均为l.若灯的大小和线的长度相比是很小的,则吊灯在垂直于纸面内作小幅振动时的悬点为点Oˊ(填写图中的字母),周期为$2π\sqrt{\frac{l+lsinα}{g}}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com