
 如图所示,可视为质点的物体AB质量均为m=10kg,它们之间用可遥控引爆的粘性炸药粘在一起.现将它们从光滑曲面上高度H=0.8m处由静止释放,曲面底端恰好和极薄的水平传送带的边缘相切.传送带两皮轮半径均为r=0.1m,均以角速度ω=30rad/s逆时针匀速转动,轮心间距为L=39.5m,皮带和轮间不打滑.已知两物体与传送带间的动摩擦因数均为μ=0.1,重力加速度g=10m/s2.则
如图所示,可视为质点的物体AB质量均为m=10kg,它们之间用可遥控引爆的粘性炸药粘在一起.现将它们从光滑曲面上高度H=0.8m处由静止释放,曲面底端恰好和极薄的水平传送带的边缘相切.传送带两皮轮半径均为r=0.1m,均以角速度ω=30rad/s逆时针匀速转动,轮心间距为L=39.5m,皮带和轮间不打滑.已知两物体与传送带间的动摩擦因数均为μ=0.1,重力加速度g=10m/s2.则分析 (1)若不启动引爆装置,AB整体在光滑曲面上下滑时,只有重力做功,机械能守恒,由机械能守恒定律求出AB刚滑到曲面底端时的速度.研究AB在传送带上运动的过程,由动量定理求得滑行时间,再结合运动学公式求解AB在水平传送带上运动的最远距离s.根据相对位移求由于摩擦而增加的内能Q;
(2)研究AB从开始到爆炸位置的过程,由动能定理求出AB的速度.对于爆炸过程,由于内力远大于外力,所以系统的动量守恒,由动量守恒定律列式.根据B到传送带右端时对传送带无压力,分析物体B的受力情况,知道重力提供向心力,由此求出B的速度.联立可求得d.
解答 解:(1)AB沿曲面下滑的过程,由机械能守恒定律得:
2mgH=$\frac{1}{2}•2m{v}_{0}^{2}$
解得:v0=$\sqrt{2gH}$=$\sqrt{2×10×0.8}$=4m/s
AB在传送带上做匀减速运动,取向右为正方向,由动量定理得:
-2μmgt=0-2mv0.
得:t=$\frac{{v}_{0}}{g}$=$\frac{4}{0.1×10}$s=4s
AB在水平传送带上运动的最远距离为:s=$\frac{{v}_{1}}{2}t$=$\frac{4}{2}$×4m=8m
传送带的位移为:s带=ωrt=30×0.1×4=12m
所以系统产生的内能为:Q=2μmg(s+s带)=2×0.1×10×10×20J=400J
(2)AB从开始到爆炸位置的过程,由动能定理得:
2mgH-2μmgd=$\frac{1}{2}•2m{v}_{1}^{2}$-0
引爆后,A必定向左运动,且速度大于3m/s,B必定向右运动,取向右为正方向,由动量守恒定律得:
2mv1=mv2-mv3.
对于A向左运动的过程,由动能定理得:
-μmgd-mgH=0-$\frac{1}{2}m{v}_{3}^{2}$
对于B向右运动的过程,由动能定理得:
-μmg(L-d)=$\frac{1}{2}m{v}_{4}^{2}$-$\frac{1}{2}m{v}_{2}^{2}$
B在传送带右端时,由牛顿第二定律得:
mg=m$\frac{{v}_{4}^{2}}{r}$
联立解得:d=$\frac{16\sqrt{5}}{5}$m
答:(1)若不启动引爆装置,AB在水平传送带上运动的最远距离s是8m,此过程中AB和传送带之间由于摩擦而增加的内能Q是400J;
(2)引爆位置d是$\frac{16\sqrt{5}}{5}$m.
点评 对于传送带类题目要注意因摩擦产生的内能等于摩擦力与相对位移间的乘积,要准确分析物体的运动情况,抓住爆炸的基本规律:动量守恒定律.


 高中必刷题系列答案
高中必刷题系列答案科目:高中物理 来源: 题型:选择题
 2015年8月25日,第12届莫斯科航展在俄罗斯莫斯科地区茹科夫斯基城开幕,在航展中,曾在2014年珠海航展上亮相过的苏-35S战斗机在莫斯科航展亮相进行飞行表演,再展“UFO”般机动性,若某次该机在一竖直面内做匀速圆周运动,则对和该机相对静止的飞行员,下列说法正确的是( )
2015年8月25日,第12届莫斯科航展在俄罗斯莫斯科地区茹科夫斯基城开幕,在航展中,曾在2014年珠海航展上亮相过的苏-35S战斗机在莫斯科航展亮相进行飞行表演,再展“UFO”般机动性,若某次该机在一竖直面内做匀速圆周运动,则对和该机相对静止的飞行员,下列说法正确的是( )| A. | 在最低点处于超重状态 | B. | 在运动过程中处于受力平衡状态 | ||
| C. | 在最高点其重力变小了 | D. | 在运动过程中机械能守恒 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示为一列沿着x轴负方向传播的简谐横波在某时刻的波形图,此时质点a的位移为20cm,质点b的平衡位置离O点的距离为$\frac{11}{12}$λ(λ为波长).经过0.1s(T>1s)质点b回到平衡位置,则( )
如图所示为一列沿着x轴负方向传播的简谐横波在某时刻的波形图,此时质点a的位移为20cm,质点b的平衡位置离O点的距离为$\frac{11}{12}$λ(λ为波长).经过0.1s(T>1s)质点b回到平衡位置,则( )| A. | 周期为1.2s | |
| B. | 从波形图所示时刻开始计时,0.6s内质点b通过的路程为0.4m | |
| C. | 当b回到平衡位置后,再经过0.2s,a回到平衡位置 | |
| D. | 波速为0.3m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,静止在光滑水平面上的木板,右端有一根轻质弹簧沿水平方向与木板相连,质量M=2kg.质量m=1kg的铁块以水平速度v0=6m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.在上述过程中弹簧具有的最大弹性势能为( )
如图所示,静止在光滑水平面上的木板,右端有一根轻质弹簧沿水平方向与木板相连,质量M=2kg.质量m=1kg的铁块以水平速度v0=6m/s,从木板的左端沿板面向右滑行,压缩弹簧后又被弹回,最后恰好停在木板的左端.在上述过程中弹簧具有的最大弹性势能为( )| A. | 3J | B. | 4J | C. | 12J | D. | 6J |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 牛顿发现了万有引力定律,并且用扭秤装置测出了引力常量 | |
| B. | 卢瑟福通过α粒子散射实验提出了原子的核式结构模型 | |
| C. | 奥斯特为了解释磁体产生的磁场提出了分子电流假说 | |
| D. | 贝克勒尔通过实验发现了中子,汤姆孙通过实验发现了质子 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 放射性元素的半衰期与元素所处环境的温度有关 | |
| B. | 现已建成的核电站发电的能量来自于轻核聚变放出的能量 | |
| C. | 某放射性原子核经过2次α衰变和1次β衰变,核内质子数减少3个 | |
| D. | 用蓝色光照射某金属表面时有电子逸出,改用紫外线照射也一定会有电子逸出 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图为甲、乙两质点同时沿同一直线运动的位移-时间图象.关于两质点的运动情况,下列说法正确的是( )
如图为甲、乙两质点同时沿同一直线运动的位移-时间图象.关于两质点的运动情况,下列说法正确的是( )| A. | 在0~t0时间内,甲、乙的运动方向相同 | |
| B. | 在0~2t0时间内,甲的速度一直在减小 | |
| C. | 在0~t0时间内,乙的速度一直增大 | |
| D. | 在0~2t0时间内,甲、乙发生的位移不相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
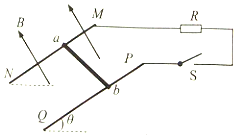 如图所示,两根足够长的平行金属导轨MN、PQ间距d=0.5m,导轨平面与水平面夹角θ=37o,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好.金属棒的质量m=2kg,电阻r=1Ω,定值电阻R=7Ω,其它电阻不计.导轨处于垂直于导轨平面向上的匀强磁场中,磁感应强度大小为B=4T.闭合开关S,金属棒由静止释放,沿斜面下滑L=0.5m时,速度v=2m/s.不计一切摩擦,sin37°=0.60,cos37°=0.80.求
如图所示,两根足够长的平行金属导轨MN、PQ间距d=0.5m,导轨平面与水平面夹角θ=37o,金属棒ab垂直于MN、PQ放置在导轨上,且始终与导轨接触良好.金属棒的质量m=2kg,电阻r=1Ω,定值电阻R=7Ω,其它电阻不计.导轨处于垂直于导轨平面向上的匀强磁场中,磁感应强度大小为B=4T.闭合开关S,金属棒由静止释放,沿斜面下滑L=0.5m时,速度v=2m/s.不计一切摩擦,sin37°=0.60,cos37°=0.80.求查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com