
 如图所示,在直角坐标系的第Ⅰ象限和第Ⅲ象限存在着电场强度均为E的匀强电场,其中第Ⅰ象限电场沿x轴正方向,第Ⅲ象限电场沿y轴负方向.在第Ⅱ象限和第Ⅳ象限存在着匀强磁场,磁场方向均垂直纸面向里.有一个电子从y轴的P点以垂直于y轴的初速度v0进入第Ⅲ象限,第一次到达x轴上时速度方向与x轴负方向夹角为45°,第一次进入第Ⅰ象限时,与y轴正方向夹角也是45°,经过一段时间电子又回到了P点,已知电子的电荷量为e,质量为m,不考虑重力和空气阻力.求:
如图所示,在直角坐标系的第Ⅰ象限和第Ⅲ象限存在着电场强度均为E的匀强电场,其中第Ⅰ象限电场沿x轴正方向,第Ⅲ象限电场沿y轴负方向.在第Ⅱ象限和第Ⅳ象限存在着匀强磁场,磁场方向均垂直纸面向里.有一个电子从y轴的P点以垂直于y轴的初速度v0进入第Ⅲ象限,第一次到达x轴上时速度方向与x轴负方向夹角为45°,第一次进入第Ⅰ象限时,与y轴正方向夹角也是45°,经过一段时间电子又回到了P点,已知电子的电荷量为e,质量为m,不考虑重力和空气阻力.求:分析 (1)电子第三象限做类平抛运动,OP为竖直方向匀加速直线运动的位移;
(2)作出粒子的运动轨迹,由轨迹知CD为粒子圆周运动的半径,根据OC的数值可以计算出CD的大小.
(3)根据几何关系求出半径,再根据洛伦兹力提供向心力求解B即可.
解答 解:(1)电子从y轴的P点以垂直于y轴的初速度v0进入第Ⅲ象限后,水平方向做匀速直线运动,竖直方向做匀加速直线运动,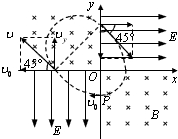 有:
有:
vy=v0tan45°=v0
又vy=at3=$\frac{eE}{m}$t3
解得:t3=$\frac{m{v}_{0}}{eE}$
PO=h=$\frac{1}{2}$at32=$\frac{1}{2}•\frac{eE}{m}•(\frac{m{v}_{0}}{eE})^{2}=\frac{m{{v}_{0}}^{2}}{2eE}$
(2)从P到C粒子做类平抛运动,水平方向位移
OC=${{v}_{0}{t}_{3}=v}_{0}\frac{eE}{m}=\frac{m{{v}_{0}}^{2}}{eE}$
由轨迹图可知,CD做匀速圆周运动,CD为圆周的直径,由几何关系可得
CD=$\sqrt{2}OC=\frac{\sqrt{2}m{{v}_{0}}^{2}}{eE}$,
(3)根据几何关系可知,粒子做匀速圆周运动的半径R=$\frac{CD}{2}=\frac{\sqrt{2}m{{v}_{0}}^{2}}{2eE}$
根据洛伦兹力提供向心力得:
Bqv=m$\frac{{{v}_{\;}}^{2}}{R}$
解得:B=$\frac{mv}{qR}=\frac{m•\sqrt{2}{v}_{0}}{e\frac{\sqrt{2}m{{v}_{0}}^{2}}{2eE}}=\frac{2E}{{v}_{0}}$
答:(1)P点距原点O的距离为$\frac{m{{v}_{0}}^{2}}{2eE}$;
(2)粒子第一次到达x轴上C点与第一次进入第Ⅰ象限时的D点之间的距离为$\frac{\sqrt{2}m{{v}_{0}}^{2}}{eE}$;
(3)第四象限匀强磁场的磁感应强度B的大小为$\frac{2E}{{v}_{0}}$.
点评 掌握平抛运动的处理方法并能运用到类平抛运动中,粒子在磁场中做匀速圆周运动,能正确的确定圆心和半径,并会根据周期公式求运动时间,难度适中.


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案科目:高中物理 来源: 题型:填空题
 在“验证机械能守恒定律”的实验中,已知打点计时器所用电源的频率为50Hz.查得当地的重力加速度g=9.80m/s2,所用的重物的质量为2kg,实验中得到一条点迹清晰的纸带,如图所示把第一个点记作O,另外连续的4个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.99cm、70.18cm、77.76cm、85.73cm.根据以上数据,可知重物由打O点运动到打C点,重力势能减少量等于15.2J,动能的增加量等于15.1J.(取三位有效数字)
在“验证机械能守恒定律”的实验中,已知打点计时器所用电源的频率为50Hz.查得当地的重力加速度g=9.80m/s2,所用的重物的质量为2kg,实验中得到一条点迹清晰的纸带,如图所示把第一个点记作O,另外连续的4个点A、B、C、D作为测量的点,经测量知道A、B、C、D各点到O点的距离分别为62.99cm、70.18cm、77.76cm、85.73cm.根据以上数据,可知重物由打O点运动到打C点,重力势能减少量等于15.2J,动能的增加量等于15.1J.(取三位有效数字)查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 一带电粒子仅在电场力作用下以初速度v0从t=0时刻开始运动,其v-t图象如图所示.如粒子在t0时刻运动到A点,5t0时刻运动到B点.以下说法中正确的是( )
一带电粒子仅在电场力作用下以初速度v0从t=0时刻开始运动,其v-t图象如图所示.如粒子在t0时刻运动到A点,5t0时刻运动到B点.以下说法中正确的是( )| A. | A、B两点的电场强度大小关系为:EA=EB | |
| B. | A、B两点的电势关系为:φA>φB | |
| C. | t0到5t0时间内,电场力做的总功为正 | |
| D. | t0到5t0时间内,电势能先减小后增大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
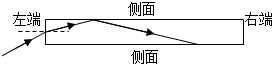 如图是一段长为L的直光导纤维内芯,一单色光从左端面射入光纤,已知光纤对单色光的折射率为n,光在真空中传播速度大小为c. 该单色光以任意不为零的入射角从左端射入,均能在侧面发生全反射,并从右端面射出.则( )
如图是一段长为L的直光导纤维内芯,一单色光从左端面射入光纤,已知光纤对单色光的折射率为n,光在真空中传播速度大小为c. 该单色光以任意不为零的入射角从左端射入,均能在侧面发生全反射,并从右端面射出.则( )| A. | 增加单色光的频率,光在光纤中的传播速度将增大 | |
| B. | 改变光在左端面的入射角,光在光纤中的传播时间不变 | |
| C. | 该单色光在光纤中传播的最短时间为$\frac{nL}{c}$ | |
| D. | n$<\sqrt{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题


查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )
如图所示,Ⅰ和Ⅱ是一对异名磁极,ab为放在其间的金属棒.ab和cd用导线连成一个闭合回路.当ab棒向左运动时,cd导线受到向下的磁场力.则有( )| A. | 由此可知d电势高于c电势 | |
| B. | 由此可知Ⅰ是S极 | |
| C. | 由此可知Ⅰ是N极 | |
| D. | 当cd棒向下运动时,ab导线受到向左的磁场力 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,C为平行板电容器,R1、R3为可变电阻,R2为定值电阻.下列哪些办法可使电容器带的电量增加(s处于闭合状态)( )
如图所示,C为平行板电容器,R1、R3为可变电阻,R2为定值电阻.下列哪些办法可使电容器带的电量增加(s处于闭合状态)( )| A. | 增大R1 | B. | 增大R3 | ||
| C. | 在电容器间加入电介质 | D. | 将两板间距离减小 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com