
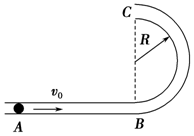
 如图所示,用细圆管组成的光滑轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,圆管截面半径r?R.有一质量为m,半径比r略小的光滑小球以水平初速度v0射入圆管.
如图所示,用细圆管组成的光滑轨道AB部分平直,BC部分是处于竖直平面内半径为R的半圆,圆管截面半径r?R.有一质量为m,半径比r略小的光滑小球以水平初速度v0射入圆管.分析 (1)当球恰好能从C端出来时,速度为零,根据机械能守恒定律求解初速度v0.
(2)以小球为研究对象,小球经过C点时速度不同,管壁对球的作用力大小和方向不同,分析讨论:当管壁对球无作用力时,在C点由重力提供小球的向心力,由牛顿第二定律求出在C点的速度,由机械能守恒定律求出初速v0.
当初速度大于和小于临界速度时,管壁对小球的压力均可以为$\frac{1}{2}$mg,由向心力知识分析管壁对球的作用力大小和方向,即可求出相应的小球的初速度v0.
解答 解:(1)选AB所在平面为参考平面,从A至C的过程中,根据机械能守恒定律:$\frac{1}{2}m{v}_{0}^{2}$=2mgR+$\frac{1}{2}m{v}_{C}^{2}$ ①
在最高点C小球速度满:足vC≥0 ②
由①②得:v0≥2$\sqrt{gR}$
(2)小球在C处受重力mg和细管竖直方向的作用力FN,根据牛顿第二定律,得:
mg+FN=m$\frac{{v}_{C}^{2}}{R}$③
由①③解得FN=m$\frac{{v}_{0}^{2}}{R}$-5mg ④
讨论④式,可得:
当小球受到向下的压力时,FN=$\frac{1}{2}$mg,v0=$\frac{\sqrt{22gR}}{2}$
当小球受到向上的压力时,FN=-$\frac{1}{2}$mg,v0=$\frac{3\sqrt{2gR}}{2}$.
答:(1)若要小球能从C端出来,初速度v0需满不小于2$\sqrt{gR}$;
(2)在小球从C端出来的瞬间,管壁对小球的压力为$\frac{1}{2}$mg,当小球受到向下的压力时v0为$\frac{\sqrt{22gR}}{2}$;当小球受到向上的压力时,v0为$\frac{3\sqrt{2gR}}{2}$.
点评 题是机械能守恒定律与向心力知识的结合,考查综合应用物理规律的能力,对于小球在管子里的运动情形与轻杆模型类似,关键抓住临界情况:小球恰好到最高点和在最高点恰好不受管壁作用力两种情况.


科目:高中物理 来源: 题型:多选题
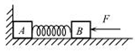 如图所示,质量分别为m和2m的 A、B两个木块间用轻弹簧相连,放在光滑水平面上,A紧靠竖直墙.用水平力F将B向左压,使弹簧被压缩一定长度,静止后弹簧储存的弹性势能为 E.这时突然撤去 F,关于A、B和弹簧组成的系统,下列说法中正确的是( )
如图所示,质量分别为m和2m的 A、B两个木块间用轻弹簧相连,放在光滑水平面上,A紧靠竖直墙.用水平力F将B向左压,使弹簧被压缩一定长度,静止后弹簧储存的弹性势能为 E.这时突然撤去 F,关于A、B和弹簧组成的系统,下列说法中正确的是( )| A. | 撤去 F 后,系统动量守恒,机械能守恒 | |
| B. | 撤去 F 后,A 离开竖直墙前,系统动量不守恒,机械能守恒 | |
| C. | 撤去 F 后,A 离开竖直墙后,弹簧的弹性势能最大值为$\frac{E}{3}$ | |
| D. | 撤去 F 后,A 离开竖直墙后,弹簧的弹性势能最大值为 E |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 2T | B. | 0.2T | C. | 5T | D. | 0.5T |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\sqrt{\frac{1+μ}{1-μ}}$v | B. | $\sqrt{\frac{1-μ}{1+μ}}$v | C. | $\sqrt{\frac{1+{μ}^{2}}{1-{μ}^{2}}}$v | D. | $\sqrt{\frac{1-{μ}^{2}}{1+{μ}^{2}}}$v |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 60J | B. | 50J | C. | 40J | D. | 30 J |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 古希腊科学家托勒密根据日常观察和经验提出“日心说” | |
| B. | 英国科学家牛顿提出了行星运动的三大定律 | |
| C. | 英国物理学家卡文迪许利用扭秤实验装置比较精确的测出了引力常量 | |
| D. | 牛顿运动定律在高速状态和微观世界仍然适用 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 光电子的最大初动能随着入射光的强度增大而增大 | |
| B. | 只要入射光的强度足够强,照射时间足够长,就一定能产生光电效应 | |
| C. | 无论光子能量大小如何,电子吸收光子并积累能量后,总能逸出成为光电子 | |
| D. | 任何一种金属都有一个极限频率,低于这个频率的光不能使它发生光电效应 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com