
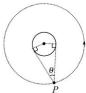
 如图所示,飞行器P绕某星球做匀速圆周运动周期为T,已知星球相对飞行器的张角为θ,引力常量为G.求该星球的密度?
如图所示,飞行器P绕某星球做匀速圆周运动周期为T,已知星球相对飞行器的张角为θ,引力常量为G.求该星球的密度? 分析 根据几何关系求出飞行器的轨道半径,结合万有引力提供向心力求出星球的质量,从而得出星球的平均密度.
解答 解:设星球的半径为R,根据几何关系知,飞行器的轨道半径为:r=$\frac{R}{sin\frac{θ}{2}}$,
根据$G\frac{Mm}{{r}^{2}}=mr\frac{4{π}^{2}}{{T}^{2}}$得星球的质量为:M=$\frac{4{π}^{2}{r}^{3}}{G{T}^{2}}$,
则星球的密度为:$ρ=\frac{M}{\frac{4π{R}^{3}}{3}}=\frac{3π{r}^{3}}{G{T}^{2}{R}^{3}}$=$\frac{3π}{G{T}^{2}si{n}^{3}\frac{θ}{2}}$.
答:星球的平均密度为$\frac{3π}{G{T}^{2}si{n}^{3}\frac{θ}{2}}$.
点评 解决本题的关键掌握万有引力提供向心力这一重要理论,并能灵活运用,知道运用该理论只能求解中心天体质量,不能求解环绕天体质量.


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:高中物理 来源: 题型:多选题
| A. | 把煤堆在墙角时间长了,墙内部也变黑,说明分子间存在间隙,且分子在无规则运动 | |
| B. | 酒精与水混合后体积减小,说明液体分子间有间隙 | |
| C. | 大风天看到风沙弥漫,尘土飞扬,这就是布朗运动 | |
| D. | 布朗运动是由于液体分子对固体小颗粒的撞击不平衡引起的 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,面积为0.2m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=(2+0.2t)T,定值电阻R1=6Ω,线圈电阻R2=4Ω,求:
如图所示,面积为0.2m2的100匝线圈处在匀强磁场中,磁场方向垂直于线圈平面,已知磁感应强度随时间变化的规律为B=(2+0.2t)T,定值电阻R1=6Ω,线圈电阻R2=4Ω,求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | “帕拉帕-D”近地点变轨前后,其轨道半长轴的三次方与周期的二次方比值不变 | |
| B. | 两卫星的设计轨道半长轴的三次方与设计周期的二次方比值相同 | |
| C. | 韩卫星坠毁过程中,卫星所受万有引力大于其做圆周运动所需向心力 | |
| D. | “帕拉帕-D”近地点变轨前后,万有引力对卫星做负功,卫星机械能不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | A的速率比B大 | B. | A的角速度比B小 | ||
| C. | A的向心加速度比B小 | D. | A的运行周期比B大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | X和Y互为同位素 | B. | Y的质量数小于X | C. | Z的电荷数大于Y | D. | Z的质量数最大 | ||||
| E. | Z的中子数小于Y |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
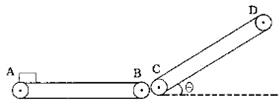 淮北水泥厂采用如图所水的装置来传送水泥,它由两台皮带传送机组成,一台水平传送,A、B两端相距x1=3.5m.另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距x2=4.45m,B、C相距很近.水平部分AB以v=5m/s的速率顺时针转动.将一袋水泥放在A端,到达B端后,速度大小不变地传到C端,水泥与两传送带间的动摩擦因数均相同.已知水泥袋从A端传到B端的时间为t=1.2s.(取g=10m/s2,sin37°=0.6,cos37°=0.8,)试求:
淮北水泥厂采用如图所水的装置来传送水泥,它由两台皮带传送机组成,一台水平传送,A、B两端相距x1=3.5m.另一台倾斜,传送带与地面的倾角θ=37°,C、D两端相距x2=4.45m,B、C相距很近.水平部分AB以v=5m/s的速率顺时针转动.将一袋水泥放在A端,到达B端后,速度大小不变地传到C端,水泥与两传送带间的动摩擦因数均相同.已知水泥袋从A端传到B端的时间为t=1.2s.(取g=10m/s2,sin37°=0.6,cos37°=0.8,)试求:查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com