
| A. | $\frac{{4{π^2}}}{g}$ | B. | $\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g}}$ | C. | $\frac{{4{π^2}(R+h)}}{g}$ | D. | $\frac{2πh}{R}\sqrt{\frac{h}{g}}$ |
分析 根据月球表面重力与万有引力相等求得黄金代换式,再根据万有引力提供圆周运动向心力求得卫星的周期.
解答 解:在月球表面有:G$\frac{Mm}{{R}^{2}}$=mg
可得:GM=gR2
绕月卫星由万有引力提供圆周运动向心力有:
G$\frac{Mm}{(R+h)^{2}}$=m(R+h)$\frac{4{π}^{2}}{{T}^{2}}$
可得卫星的周期为:
T=$2π\sqrt{\frac{(R+h)^{3}}{GM}}$=$\frac{2π(R+h)}{R}\sqrt{\frac{R+h}{g}}$
故选:B
点评 解决本题抓住星球表面重力与万有引力相等,万有引力提供卫星圆周运动向心力,用好黄金代换式是关键.


科目:高中物理 来源: 题型:解答题
 如图,在光滑水平面上有一质量为M=4kg且足够长的木板,一质量为m=0.9kg的木块放于木板左端,木块与木板间动摩擦因数为μ=0.2,开始时木块与木板间均处于静止状态.现在一质量为m0=0.1kg的子弹以速度为v0=100m/s水平射入木块且未穿出,设子弹射入木块过程时间极短,求木块在木板上相对木板滑行的距离s.
如图,在光滑水平面上有一质量为M=4kg且足够长的木板,一质量为m=0.9kg的木块放于木板左端,木块与木板间动摩擦因数为μ=0.2,开始时木块与木板间均处于静止状态.现在一质量为m0=0.1kg的子弹以速度为v0=100m/s水平射入木块且未穿出,设子弹射入木块过程时间极短,求木块在木板上相对木板滑行的距离s.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
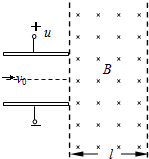 如图所示,偏转电场的两个平行极板水平放置,偏转电场的场强E=2.4×10-3V•m-1,板长L=0.08m,板距足够大,两板的右侧有水平宽度l=0.06m、竖直宽度足够大的有界匀强磁场.一个比荷为$\frac{q}{m}$=5×107 C/kg的粒子(其重力不计)以v0=80m/s速度从两板中间沿与板平行的方向射入偏转电场,离开偏转电场后进入匀强磁场,最终垂直右边界射出.求:
如图所示,偏转电场的两个平行极板水平放置,偏转电场的场强E=2.4×10-3V•m-1,板长L=0.08m,板距足够大,两板的右侧有水平宽度l=0.06m、竖直宽度足够大的有界匀强磁场.一个比荷为$\frac{q}{m}$=5×107 C/kg的粒子(其重力不计)以v0=80m/s速度从两板中间沿与板平行的方向射入偏转电场,离开偏转电场后进入匀强磁场,最终垂直右边界射出.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,水平转盘的中心有个竖直小圆筒,质量为m的物体A放在转盘上,A到竖直筒中心的距离为r.物体A通过轻绳、无摩擦的滑轮与物体B相连,B与A质量相同.物体A与转盘间的摩擦系数为μ(最大静摩擦力等于滑动摩擦力),则转盘转动的角速度在什么范围内,物体A才能随盘转动.
如图所示,水平转盘的中心有个竖直小圆筒,质量为m的物体A放在转盘上,A到竖直筒中心的距离为r.物体A通过轻绳、无摩擦的滑轮与物体B相连,B与A质量相同.物体A与转盘间的摩擦系数为μ(最大静摩擦力等于滑动摩擦力),则转盘转动的角速度在什么范围内,物体A才能随盘转动.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 1.6 m | B. | 2.4 m | C. | 3.2 m | D. | 4.0 m |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,光滑半球形容器固定在水平面上,O为球心.一质量为m的小滑块,在水平力F的作用下静止于P点.设滑块所受支持力为FN,OP与水平方向的夹角为θ=30°.下列正确的是( )
如图所示,光滑半球形容器固定在水平面上,O为球心.一质量为m的小滑块,在水平力F的作用下静止于P点.设滑块所受支持力为FN,OP与水平方向的夹角为θ=30°.下列正确的是( )| A. | F=$\frac{{\sqrt{3}mg}}{3}$ | B. | F=$\sqrt{3}$mg | C. | FN=$\frac{{2\sqrt{3}mg}}{3}$ | D. | FN=$\frac{{\sqrt{3}mg}}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,A、B带电小球电量分别为+q和-q,质量均为m,两球用丝线连接,A球又以丝线挂在O点,再加一个场强为E,方向水平向左的匀强电场,当平衡后两线都被拉紧,求上段丝线上的拉力并判断下段丝线拉力大小的范围.
如图所示,A、B带电小球电量分别为+q和-q,质量均为m,两球用丝线连接,A球又以丝线挂在O点,再加一个场强为E,方向水平向左的匀强电场,当平衡后两线都被拉紧,求上段丝线上的拉力并判断下段丝线拉力大小的范围.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 在“研究平抛物体的运动”的实验中
在“研究平抛物体的运动”的实验中查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com