
在竖直平面内有一半径为R的光滑圆环轨道,一质量为m的小球穿在圆环轨道上做圆周运动,到达最高点C时的速率vc=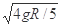 ,则下述正确的是( )
,则下述正确的是( )
A.此球的最大速率是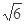 vc vc |
B.小球到达C点时对轨道的压力是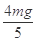 |
| C.小球在任一直径两端点上的动能之和相等 |
D.小球沿圆轨道绕行一周所用的时间小于π |
ACD
解析试题分析:因为圆环轨道是光滑的,只有重力做功,所以机械能守恒,可以求得在最低点时的最大速度;
对物体受力分析,根据圆周运动的向心力公式可以求得对轨道的作用力,由周期公式可以知道物体运动的周期.
解:A、速度最大的点应该是最低点时,根据动能定理: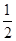 mV2-
mV2-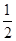 mVc2=2mgR,解得
mVc2=2mgR,解得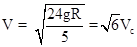 ,所以A正确.
,所以A正确.
B、在C点有: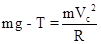 ,得T=
,得T=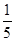 mg,所以B错误.
mg,所以B错误.
C、整个过程中机械能守恒,在任一直径两端点上的点,它们的高度之和都是2R,即它们的重力势能的和相等,由于总的机械能守恒,所以它们的动能之和也相等,所以C正确.
D、由 ,当速度最小时,代入计算可得
,当速度最小时,代入计算可得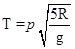 ,之后小球的速度在变大,所以T要减小,所以
,之后小球的速度在变大,所以T要减小,所以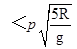 ,所以D正确.
,所以D正确.
故选ACD.
考点:机械能守恒定律;牛顿第二定律;向心力.
点评:小球穿在圆环轨道上做圆周运动,属于杆的模型,在最高点时速度最小,向心力最小,最低点时速度最大,向心力最大,由机械能守恒可以求它们之间的关系.


 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案科目:高中物理 来源: 题型:
 如图所示,在竖直平面内有一半径为2.0m的l/4圆弧形光滑导轨AB,A点与其最低点C的高度差为1.0m,今由A点沿导轨无初速释放一个小球,若取g=10m/s2,则( )
如图所示,在竖直平面内有一半径为2.0m的l/4圆弧形光滑导轨AB,A点与其最低点C的高度差为1.0m,今由A点沿导轨无初速释放一个小球,若取g=10m/s2,则( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=3R,重力加速度为g,则小球从P到B的运动过程中( )
如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=3R,重力加速度为g,则小球从P到B的运动过程中( )查看答案和解析>>
科目:高中物理 来源: 题型:
 如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )
如图所示,在竖直平面内有一半径为R的圆弧轨道,半径OA水平、OB竖直,一个质量为m的小球自A的正上方P点由静止开始自由下落,小球沿轨道到达最高点B时恰好对轨道没有压力.已知AP=2R,重力加速度为g,则小球从P到B的运动过程中( )查看答案和解析>>
科目:高中物理 来源: 题型:
 (2009?安庆三模)在竖直平面内有一半径为R的光滑圆环轨道,一质量为m的小球穿在圆环轨道上做圆周运动,到达最高点C时的速率vc=
(2009?安庆三模)在竖直平面内有一半径为R的光滑圆环轨道,一质量为m的小球穿在圆环轨道上做圆周运动,到达最高点C时的速率vc=
|
查看答案和解析>>
科目:高中物理 来源: 题型:
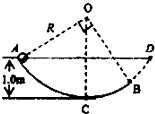 如图所示,在竖直平面内有一半径为2m的
如图所示,在竖直平面内有一半径为2m的| 1 |
| 4 |
A、小球过B点的速度vB=2
| ||||
B、小球过B点的速度vB=2
| ||||
| C、小球离开B点后做平抛运动 | ||||
| D、小球离开B点后将继续运动到与A、D等高的位置 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com