
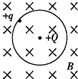
 如图所示,磁场中固定一正点电荷+Q,一个质子以+Q为圆心在匀强磁场中做匀速圆周运动.磁场方向垂直于质子的运动平面,磁感强度的大小为B,若质子所受磁场力是电荷+Q作用的电场力的三倍,质子的电荷量为q、质量为m.则质子运动的角速度可能是( )
如图所示,磁场中固定一正点电荷+Q,一个质子以+Q为圆心在匀强磁场中做匀速圆周运动.磁场方向垂直于质子的运动平面,磁感强度的大小为B,若质子所受磁场力是电荷+Q作用的电场力的三倍,质子的电荷量为q、质量为m.则质子运动的角速度可能是( )| A. | $\frac{2Bq}{3m}$ | B. | $\frac{2Bq}{m}$ | C. | $\frac{3Bq}{m}$ | D. | $\frac{4Bq}{m}$ |
分析 由于不知道磁电荷运动方向,但是知道洛伦兹力和速度垂直,因此分顺时针和逆时针两种转动情况进行分析,然后根据向心力公式以及线速度和角速度的关系列方程即可求解.
解答 解:该题中,质子可能有两种绕行的方向;
1、若顺时针,则质子受到的洛伦兹力的方向向外,由于质子受到正电荷的斥力,所以合力的方向向外,质子不可能做圆周运动.
2、若粒子逆时针转动,则质子受到的洛伦兹力的方向向里,由于质子受到正电荷的斥力,所以合力的方向向里,质子做圆周运动,由于质子所受洛伦兹力是电场力的3倍,即:qvB=3qE,合力提供向心力,即:qvB-$\frac{1}{3}$qvB=mω2r=mv•ω
所以:ω=$\frac{2Bq}{3m}$;
故选:A.
点评 本题在电磁场中结合电场力和洛伦兹力考查了圆周运动问题,关键是熟练运用向心力公式的各种表达式正确解答,本题应明确洛伦兹力和电场力的合力充当向心力,从而求出对应的角速度.


科目:高中物理 来源: 题型:计算题
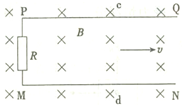 如图所示,平行金属导轨PQ、MN相距L=0.80m,PM间接有R=4.0Ω的电阻,匀强磁场与PQMN平面垂直,磁感应强度B=1.0T,导体棒cd沿导轨平面向右匀速运动,在回路中产生的电流I=0.50A.求:
如图所示,平行金属导轨PQ、MN相距L=0.80m,PM间接有R=4.0Ω的电阻,匀强磁场与PQMN平面垂直,磁感应强度B=1.0T,导体棒cd沿导轨平面向右匀速运动,在回路中产生的电流I=0.50A.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
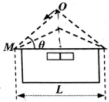 建造房屋时,一般保持底边L不变,要设计好屋顶的倾角θ,以便下雨时落在屋顶的雨滴能尽可能地滑离屋顶,其简化模型如图.设雨滴下滑时可视为无摩擦的运动,从顶端O下滑到屋檐M的时间为t,到达M点速度为v,则( )
建造房屋时,一般保持底边L不变,要设计好屋顶的倾角θ,以便下雨时落在屋顶的雨滴能尽可能地滑离屋顶,其简化模型如图.设雨滴下滑时可视为无摩擦的运动,从顶端O下滑到屋檐M的时间为t,到达M点速度为v,则( )| A. | θ越大,v越大 | B. | θ越小,v越大 | C. | θ越大,t越大 | D. | θ越小,t越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 牛顿认为力的真正效应是维持物体的速度 | |
| B. | 牛顿巧妙地利用扭秤装置,第一次在实验室里测出了引力常量的数值 | |
| C. | 牛顿提出的万有引力定律奠定了天体力学的基础 | |
| D. | 经典力学的建立标志着近代自然科学进入了微观世界 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 两者的振动周期都不变 | |
| B. | 两者的振动周期都变小 | |
| C. | 单摆的振动周期变小,弹簧振子的振动周期不变 | |
| D. | 单摆的振动周期变小,弹簧振子的振动周期变大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,倾角θ=30°的固定斜面上固定着挡板,轻弹簧下端与挡板相连,弹簧处于原长时上端位于D点.用一根不可伸长的轻绳通过轻质光滑定滑轮连接物体A和B,使滑轮左侧绳子始终与斜面平行,初始时A位于斜面的C点,C、D两点间的距离为L.现由静止同时释放A、B,物体A沿斜面向下运动,将弹簧压缩到最短的位置为E点,D、E两点间距离为$\frac{L}{2}$.若A、B的质量分别为4m和m,A与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{8}$,不计空气阻力,重力加速度为g.整个过程中,轻绳始终处于伸直状态,则( )
如图所示,倾角θ=30°的固定斜面上固定着挡板,轻弹簧下端与挡板相连,弹簧处于原长时上端位于D点.用一根不可伸长的轻绳通过轻质光滑定滑轮连接物体A和B,使滑轮左侧绳子始终与斜面平行,初始时A位于斜面的C点,C、D两点间的距离为L.现由静止同时释放A、B,物体A沿斜面向下运动,将弹簧压缩到最短的位置为E点,D、E两点间距离为$\frac{L}{2}$.若A、B的质量分别为4m和m,A与斜面之间的动摩擦因数μ=$\frac{\sqrt{3}}{8}$,不计空气阻力,重力加速度为g.整个过程中,轻绳始终处于伸直状态,则( )| A. | A在从C至E的过程中,先做匀加速运动,后做匀减速运动 | |
| B. | A在从C至D的过程中,加速度大小为$\frac{1}{20}$g | |
| C. | 弹簧的最大弹性势能为$\frac{3}{8}$mgL | |
| D. | 弹簧的最大弹性势能为$\frac{15}{8}$mgL |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com