
| 1 |
| 2 |
| v | 22 |
| ||
| R |
| R-H |
| R |
| H-0.2 |
| sinθ |
| 1 |
| 2 |
| 4 |
| 3 |
| v2 |
| R |
| v2 |
| R |
2mg-
| ||
| R |
| 0.8 |
| 3 |
2mg-
| ||
| R |


科目:高中物理 来源: 题型:
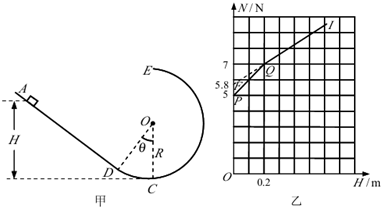
 (2013?河池模拟)如图甲所示,一竖直平面内的轨道由粗糙斜面AD和光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,将一小物块置于轨道ADC上离地面高为H处由静止释放,用力传感器测出其经过C点时对轨道的压力N,改变H的大小,
(2013?河池模拟)如图甲所示,一竖直平面内的轨道由粗糙斜面AD和光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,将一小物块置于轨道ADC上离地面高为H处由静止释放,用力传感器测出其经过C点时对轨道的压力N,改变H的大小,查看答案和解析>>
科目:高中物理 来源: 题型:
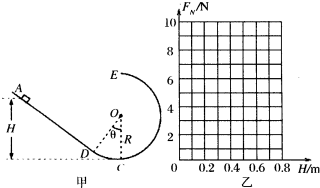 如图甲所示,一竖直平面内的轨道由粗糙斜面AD和半径R=lm的光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,轨道DC所对应的圆心角θ=37°,将一质量m=0.5kg的小物块置于轨道ADC上离地面高为H=0.7m处由静止释放,经过C点时对轨道的压力FN=10N.已知sin37°=0.6,cos37°=0.8,g取10m/s2.
如图甲所示,一竖直平面内的轨道由粗糙斜面AD和半径R=lm的光滑圆轨道DCE组成,AD与DCE相切于D点,C为圆轨道的最低点,轨道DC所对应的圆心角θ=37°,将一质量m=0.5kg的小物块置于轨道ADC上离地面高为H=0.7m处由静止释放,经过C点时对轨道的压力FN=10N.已知sin37°=0.6,cos37°=0.8,g取10m/s2.查看答案和解析>>
科目:高中物理 来源: 题型:
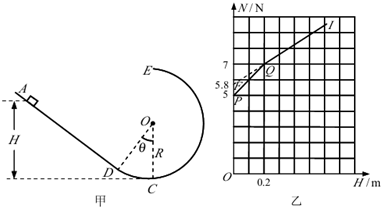
查看答案和解析>>
科目:高中物理 来源:2008-2009学年江苏省苏州、五锡、常州、镇江高三(上)教学情况调查物理试卷(解析版) 题型:解答题
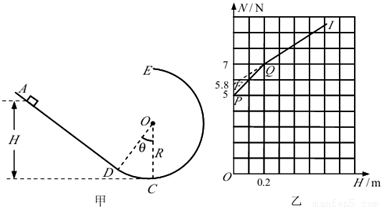
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com