
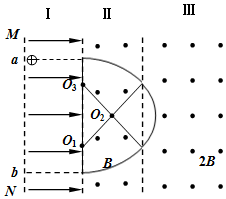
 如图,虚线是场区的分界面,竖直而平行,Ⅰ区是水平向右的匀强电场,电场强度是E,场区宽度是L,Ⅱ、Ⅲ区都是垂直纸面向外的匀强磁场,磁感应强度分别B和2B,一个电荷量是q、质量是m的正电荷,不计重力,从MN边界上的a点静止开始运动,通过磁场区Ⅱ时,速度方向偏转了30°,进入磁场区Ⅲ后,能按某一路径返回到电场区Ⅰ的边界MN上的某一点b,(b点未画出),求此粒子从a回到b的整个过程.
如图,虚线是场区的分界面,竖直而平行,Ⅰ区是水平向右的匀强电场,电场强度是E,场区宽度是L,Ⅱ、Ⅲ区都是垂直纸面向外的匀强磁场,磁感应强度分别B和2B,一个电荷量是q、质量是m的正电荷,不计重力,从MN边界上的a点静止开始运动,通过磁场区Ⅱ时,速度方向偏转了30°,进入磁场区Ⅲ后,能按某一路径返回到电场区Ⅰ的边界MN上的某一点b,(b点未画出),求此粒子从a回到b的整个过程.分析 (1)粒子在第一次离开电场时的速度最大,根据动能定理可求得最大速度;
(2)分析粒子的运动过程,分别由求在电场和磁场中的运动时间即可求得总时间,注意在磁场中要注意找出圆心和半径,从而确定转过的圆心角;
(3)根据作出的运动轨迹图进行分析,由几何关系即可确定对应的距离.
解答 解:
(1)当粒子离开电场时的速度达最大,则有动能定理可得:
$qEL=\frac{1}{2}m{v^2}$
解得:
$v=\sqrt{\frac{2qEL}{m}}$
(2)粒子在电场中的运动时间t1=$\frac{2L}{\frac{v}{2}}$=2$\sqrt{\frac{2mL}{qE}}$;
由周期公式可得:T1=$\frac{2πm}{Bq}$;
T2=$\frac{πm}{Bq}$
粒子在磁场中运动轨迹如题图所示;
粒子在磁场区Ⅱ中是两段圆心角是30°的圆弧,在磁场区Ⅲ中是一段圆心角是120°的圆弧
则可知磁场中的总时间t'=2×$\frac{30}{360}×\frac{2πm}{Bq}$+$\frac{120}{360}×\frac{πm}{Bq}$=$\frac{2πm}{3qB}$
所以总时间:$t=2\sqrt{\frac{2mL}{qE}}+\frac{2π\;m}{3qB}$
(3)由R=$\frac{mv}{Bq}$可得:
粒子第一次通过磁场区Ⅱ时圆心是O1,圆半径RⅡ=$\frac{1}{B}\sqrt{\frac{2mEL}{q}}$,
通过磁场区Ⅲ时半径减半,圆心是O2,RⅢ=$\frac{1}{2B}\sqrt{\frac{2mEL}{q}}$,
第二次通过磁场区Ⅱ时圆心是O3,半径为RⅡ不变
由几何关系可知:
ab=2RⅡ(1-cos30°)+2RⅢcos30°=$\frac{{4-\sqrt{3}}}{B}\sqrt{\frac{mEL}{2q}}$
答:(1)最大速度为$\sqrt{\frac{2qEL}{m}}$
(2)运动时间为2$\sqrt{\frac{2mL}{qE}}$+$\frac{2πm}{3qB}$
(3)ab间的距离为$\frac{{4-\sqrt{3}}}{B}\sqrt{\frac{mEL}{2q}}$
点评 本题考查带电粒子在磁场和电场中的运动规律,要注意正确分析物理过程,在电场中优先利用动能定理进行分析,而在磁场中要注意正确应用几何关系确定圆心和半径,牢记半径公式和周期公式即可分析求解.


科目:高中物理 来源: 题型:多选题
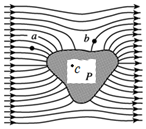 不带电导体P置于电场中,其周围电场线分布如图所示,a、b为电场中的两点,c点为导体内部的点,下列说法正确的是( )
不带电导体P置于电场中,其周围电场线分布如图所示,a、b为电场中的两点,c点为导体内部的点,下列说法正确的是( )| A. | a点电场强度小于b点电场强度 | |
| B. | c点电场强度小于b点电场强度 | |
| C. | 负检验电荷在a点的电势能比在b点的大 | |
| D. | 导体P表面处的电场线与导体表面垂直 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | “第3s内”是一个时刻 | |
| B. | 汽车以20km/h的速度通过一段路,这个速度是“平均速度” | |
| C. | “位移”大小总是等于路程大小,方向由初位置指向末位置 | |
| D. | “加速度”是描述速度变化大小的物理量,它是矢量 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 质点受同一水平面内四个共点力作用处于静止状态.F1=3N,F3=6N和未知大小的F2、F4,其方向如图所示.当撤去F2和F3后,质点在光滑水平面上运动时间t=10s,发生的位移s=100m.求:
质点受同一水平面内四个共点力作用处于静止状态.F1=3N,F3=6N和未知大小的F2、F4,其方向如图所示.当撤去F2和F3后,质点在光滑水平面上运动时间t=10s,发生的位移s=100m.求:查看答案和解析>>
科目:高中物理 来源: 题型:计算题
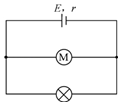 图中电源电动势E=12V,内电阻r=0.5Ω,将一盏额定电压为8V,额定功率为16W的灯泡与一只线圈电阻为0.5Ω的直流电动机并联后和电源相连,灯泡刚好正常发光,通电100min,问:
图中电源电动势E=12V,内电阻r=0.5Ω,将一盏额定电压为8V,额定功率为16W的灯泡与一只线圈电阻为0.5Ω的直流电动机并联后和电源相连,灯泡刚好正常发光,通电100min,问:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 开普勒通过对行星运动规律的研究总结出了万有引力定律 | |
| B. | 将物体视质点,采用了等效替代法 | |
| C. | 用比值法来描述加速度这个物理量,其表达式a=$\frac{F}{m}$ | |
| D. | 卡文迪许通过扭秤装置实验测出了万有引力常量 |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图,一段导线abcd位于磁感应强度大小为B的匀强磁场中,且与磁场方向(垂直于纸面向里)垂直.线段ab、bc和cd的长度均为L,且∠abc=∠bcd=150°.流经导线的电流为i,方向如图中箭头所示.导线段abcd所受到的磁场的作用力的合力( )
如图,一段导线abcd位于磁感应强度大小为B的匀强磁场中,且与磁场方向(垂直于纸面向里)垂直.线段ab、bc和cd的长度均为L,且∠abc=∠bcd=150°.流经导线的电流为i,方向如图中箭头所示.导线段abcd所受到的磁场的作用力的合力( )| A. | 方向沿纸面向上,大小为($\sqrt{3}$+1)ILB | B. | 方向沿纸面向上,大小为($\sqrt{3}$-1)ILB | ||
| C. | 方向沿纸面向下,大小为($\sqrt{3}$+1)ILB | D. | 方向沿纸面向下,大小为($\sqrt{3}$-1)ILB |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com