
���� ��1�������������������������ɷֱ��������������������
��2�������������ṩ����������������ڣ�
��3�����������ṩ���������ɷֱ�������ֵ�һ�����ٶȣ�
��� �⣺��1�������ǵ�����Ϊm��G��ʾ���������������ڵ�����棺$mg=\frac{G{M}_{��}m}{{R}_{1}^{2}}$ ��
���ԣ�M��=$\frac{g{R}_{1}^{2}}{G}$ ��
�ڵ�����棺mg=G1 ��
��������棺mg��=G2 ��
�����ۢܵã�${g}_{��}=\frac{{G}_{2}}{{G}_{1}}•g$ ��
����������Ϊ${M}_{��}^{\;}$������������������������$m{g}_{��}=\frac{G{M}_{��}m}{{R}_{2}^{2}}$ ��
��ã�${M}_{��}=\frac{{g}_{��}{R}_{2}^{2}}{G}$=$\frac{{G}_{2}{R}_{2}^{2}g}{{G}_{1}G}$ ��
�����ã�$\frac{{M}_{��}}{{M}_{��}}$=$\frac{{G}_{2}{R}_{2}^{2}}{{G}_{1}{R}_{1}^{2}}$
��2������������������ṩ���������У�$m{g}_{��}=\frac{m•4{��}^{2}{R}_{2}}{{T}^{2}}$ ��
���ԣ�T=$\sqrt{\frac{4{��}^{2}{R}_{2}}{{g}_{��}}}$=$2��\sqrt{\frac{{R}_{2}{G}_{1}}{{G}_{2}g}}$
��3�����ݵ�����������ṩ���������У�$mg=\frac{m{v}_{1}^{2}}{{R}_{1}}$��
���ԣ�${v}_{1}=\sqrt{g{R}_{1}}$
����������������ṩ���������У�$m{g}_{��}=\frac{m{v}_{2}^{2}}{{R}_{2}}$
���ԣ�${v}_{2}=\sqrt{{g}_{��}{R}_{2}}$=$\sqrt{\frac{{G}_{2}}{{G}_{1}}•g{R}_{2}}$
���ԣ�$\frac{{v}_{2}}{{v}_{1}}=\sqrt{\frac{{G}_{2}{R}_{2}}{{G}_{1}{R}_{1}}}$
�𣺣�1���������������������֮����$\frac{{G}_{2}{R}_{2}^{2}}{{G}_{1}{R}_{1}^{2}}$��
��2���϶��ĺ��ڽ������������������Բ���˶�������$2��\sqrt{\frac{{R}_{2}{G}_{1}}{{G}_{2}g}}$��
��3������ĵ�һ�����ٶ������ĵ�һ�����ٶ�֮����$\sqrt{\frac{{G}_{2}{R}_{2}}{{G}_{1}{R}_{1}}}$��
���� �������Ĺؼ����������������ɵ�������Ҫ���ۣ�1�����������ṩ��������2������������������������������ã�


 ������ϰ�ο����뵥Ԫ���ϵ�д�
������ϰ�ο����뵥Ԫ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
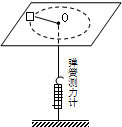 �����Ƶ���������Բ���˶�������ȫʧ��״̬�����������ֻ�������������ƽ�������������������ijͬѧ�����ֻ����������ͼ��ʾ��װ�ã�ͼ��OΪ�⻬��С�ף����������������������������һ�����ٶȣ�ʹ����ˮƽ������������Բ���˶����躽�����о��л����IJ������ߣ�
�����Ƶ���������Բ���˶�������ȫʧ��״̬�����������ֻ�������������ƽ�������������������ijͬѧ�����ֻ����������ͼ��ʾ��װ�ã�ͼ��OΪ�⻬��С�ף����������������������������һ�����ٶȣ�ʹ����ˮƽ������������Բ���˶����躽�����о��л����IJ������ߣ��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �ӵ����ǹ�ڵ��ٶ���800 m/s���� 790 m/s���ٶȻ���Ŀ�ָ꣬����˲ʱ�ٶ� | |
| B�� | �����Ӽ�վ��ʻ����վ���ٶ���40 km/h��ָ����˲ʱ�ٶ� | |
| C�� | ����ͨ��վ��ʱ���ٶ���72 km/h��ָ����ƽ���ٶ� | |
| D�� | С���3 s�ڵ��ٶ���6 m/s��ָ����ƽ���ٶ� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �ڲ���Ҫ�������屾���Ĵ�С����״ʱ�����ʵ�����������ķ����м��跨 | |
| B�� | �����ٶȶ���ʽv=$\frac{��x}{��t}$������t�dz��dz�Сʱ��$\frac{��x}{��t}$�Ϳ��Ա�ʾ������tʱ�̵�˲ʱ�ٶȣ��ö���Ӧ���˼���˼ά�� | |
| C�� | ����ƿ��װ��ˮ���ô�����ϸ�ܵ���Ƥ���ڣ�������ƿ��ϸ����Һ��߶ȱ仯��˵������ƿ�����α䣬��ʵ����÷Ŵ��˼�� | |
| D�� | ���Ƶ��ȱ����˶�λ�ƹ�ʽʱ���������˶����̻��ֳɺܶ�С�Σ�ÿһС�ν��ƿ�������ֱ���˶���Ȼ��Ѹ�С�ε�λ����ӣ����������Ԫ�� | |
| E�� | ţ������������������ɣ����������̫���͵���֮������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��

| A�� | �ڵ�1sĩ�����λ�Ƹı䷽�� | B�� | ��1sĩ����ļ��ٶȸı䷽�� | ||
| C�� | �ڵ�2sĩ�����λ�Ƹı䷽�� | D�� | �ڵ�2sĩ������ٶȸı䷽�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
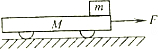 ��ͼ��ʾ������M=4kg��С������ˮƽ���ϣ���С���Ҷ˼�һF=16N��ˮƽ��������С�������˶����ٶȴﵽ4m/sʱ����С��ǰ������ط�һ����С���ƶ���Ϊm=4kg��С��飬�����С����Ķ�Ħ��������1=0.1��С����ˮƽ��䶯Ħ��������2=0.2������F����5s��ȥ����
��ͼ��ʾ������M=4kg��С������ˮƽ���ϣ���С���Ҷ˼�һF=16N��ˮƽ��������С�������˶����ٶȴﵽ4m/sʱ����С��ǰ������ط�һ����С���ƶ���Ϊm=4kg��С��飬�����С����Ķ�Ħ��������1=0.1��С����ˮƽ��䶯Ħ��������2=0.2������F����5s��ȥ�����鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ��ͼ��ʾ��ab�������뵼�ߡ���������������ɱպϻ�·������˵����ȷ���ǣ�������
��ͼ��ʾ��ab�������뵼�ߡ���������������ɱպϻ�·������˵����ȷ���ǣ�������| A�� | ��ab�������˶�ʱ����������ָ��ƫת���綯���Ǹ������ԭ�������� | |
| B�� | ��ab�������˶�ʱ����������ָ��ƫת��������Ǹ������ԭ�������� | |
| C�� | ��ab���شŸ��߷����˶�ʱ����������ָ��ƫת���綯���Ǹ������ԭ�������� | |
| D�� | ��ab���شŸ��߷����˶�ʱ����������ָ��ƫת��������Ǹ������ԭ�������� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
 ͼ��ʵ����һ�鲻֪�������ǿ�糡�ĵ糡�ߣ���2��10-6C�ĸ���ɴ�A����ˮƽ�����Ƶ�B�㣬�糡������2��10-6J�Ĺ���A��B��������Ϊ2cm����
ͼ��ʵ����һ�鲻֪�������ǿ�糡�ĵ糡�ߣ���2��10-6C�ĸ���ɴ�A����ˮƽ�����Ƶ�B�㣬�糡������2��10-6J�Ĺ���A��B��������Ϊ2cm�����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com