

分析 (1)由洛伦兹力提供向心力可以得到轨道半径,由轨道半径可得周期,由磁场的变化可以画出在第一段时间内粒子的运动轨迹,由运动轨迹的几何关系可得到粒子的坐标.
(2)依据第一问得到的结果,可以得到在第二,第三时间段内的运动轨迹,由图可知粒子恰好在第三段时间末到达y轴,由此可得时间
(3)依据磁场变化的周期性,可知粒子的运动也存在对应的周期性,可做粒子的轨迹图,由图可知其返回的时间.
解答 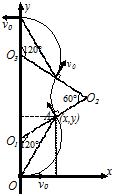 解:(1)粒子进入磁场后在磁场中作圆周运动,设半径为R,周期为T,由洛仑兹力提供向心力,
解:(1)粒子进入磁场后在磁场中作圆周运动,设半径为R,周期为T,由洛仑兹力提供向心力,
有qvB=$m\frac{v2}{R}$ 得:R=$\frac{mv}{qB}$=$\frac{2×103×10-4}{0.5}$=0.4m
又T=$\frac{2πR}{v}$=$\frac{2πm}{qB}$=$\frac{2π×10-4}{0.5}$=4π×10-4s
在磁场变化的第一段时间内,粒子运动的周期数为:N=$\frac{1}{3}$(个运动周期)运动轨迹对应的圆心角为120°,作出粒子在磁场中运动的轨迹如图所示.第一段时间末,粒子的坐标为:
x=Rcos30°=0.2$\sqrt{3}$m,y=R+$\overline{{O}_{1}A}$sin30°=0.6m
所求时刻,粒子的坐标(0.2$\sqrt{3}$m,0.6m)
(2)根据第(1)问可知,粒子在第一个磁场变化的时间段内时,运动了N1=$\frac{1}{3}$个周期,在第二个时间段内运动的周期数为N2=$\frac{1}{6}$(个周期)
所对应的运动轨迹圆心角为60°.运动轨迹如图所示.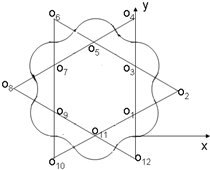
第三个时间段内同样运动了:N3=$\frac{1}{3}$(个周期),
对应的圆心角为120°粒子运动轨迹如图,粒子恰好在第三段时间末通过y轴故运动时间为t=$\frac{π}{3}$×10-3s s
(3)粒子在磁场中作周期性运动,根据对称性和周期性,画出粒子的部分运动轨迹如图,其中O2、O6、O10构成一个正三边形.
故粒子在磁场中一共运动了6个大圆弧和6个小圆弧,故从原点出发到回到原点的总时间为t'=6×$\frac{4π}{3}$×10-4s+6×$\frac{2π}{3}$×10-4s=12π×10-4s
答:(1)t=$\frac{4π}{3}$×10-4s时刻,粒子的坐标(0.2$\sqrt{3}$m,0.6m).
(2)粒子从开始时刻起经运动时间为为$\frac{π}{3}$×10-3s 到达y轴.
(3)粒子可以返回原点,所经历的时间为12π×10-4s
点评 本题重点是对磁场周期性的应用,磁场的周期性一定就会由粒子运动周期性的变化,故只要得到一个周期的运动轨迹,就可以重复画轨迹,直到得到想要的结果.本题由于粒子的运动轨迹比较复杂,故考察的难度相对较大.


科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,放在水平桌面上的木块A处于静止状态,所挂的砝码和托盘的总质量为0.6kg,弹簧测力计读书为2N,滑轮摩擦不计,若轻取走盘中的部分砝码,使总质量减少到0.3kg时,将会出现的情况是(g=10m/s2)( )
如图所示,放在水平桌面上的木块A处于静止状态,所挂的砝码和托盘的总质量为0.6kg,弹簧测力计读书为2N,滑轮摩擦不计,若轻取走盘中的部分砝码,使总质量减少到0.3kg时,将会出现的情况是(g=10m/s2)( )| A. | A仍静止不动 | B. | 弹簧测力计的读数将变小 | ||
| C. | A对桌面的摩擦力不变 | D. | A所受的合力将要变大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| 速度m/s | 反应距离m | 制动距离m |
| 15 | 18 | 45 |
| 20 | X | 80 |
| 25 | 30 | 125 |
| A. | X=20 | B. | X=22 | C. | X=24 | D. | X=26 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
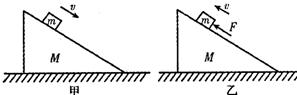
| A. | F2>F,F1=0 | B. | F1>F,F2=0 | C. | F>F1,F2=0 | D. | F>F2,F1=0 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
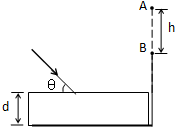 如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.保留两位有效数字.试求:
如图所示,真空中有一下表面镀反射膜的平行玻璃砖,其折射率n=$\sqrt{2}$,一束单色光与界面成θ=45°角斜射到玻璃砖表面上,最后在玻璃砖的右侧面竖直光屏上出现了两个光点A和B,A和B相距h=2.0cm.已知光在真空中的传播速度c=3.0×108m/s.保留两位有效数字.试求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 甲、乙两物体同时、同向出发,两物体运动的速度图象如图,甲先加速后减速,乙一直匀速,出发时甲在乙的前方,x=1.5m处,两物体相遇而不相碰,求:
甲、乙两物体同时、同向出发,两物体运动的速度图象如图,甲先加速后减速,乙一直匀速,出发时甲在乙的前方,x=1.5m处,两物体相遇而不相碰,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
 如图所示,一理想变压器原线圈接入一交流电源,副线圈电路中R1、R2、R3和R4均为定值电阻,开关S是断开的,V1.V2为理想电压表,读数分别为U1和U2;Al、A2和A3为理想电流表,读数分别为I1、I2和I3.现闭合S,如果保持U1数值不变,下列推断中正确的是( )
如图所示,一理想变压器原线圈接入一交流电源,副线圈电路中R1、R2、R3和R4均为定值电阻,开关S是断开的,V1.V2为理想电压表,读数分别为U1和U2;Al、A2和A3为理想电流表,读数分别为I1、I2和I3.现闭合S,如果保持U1数值不变,下列推断中正确的是( )| A. | U2变小、I3变小 | B. | U2不变、I2变大 | C. | I1变大、I2变大 | D. | I1变大、I3变大 |
查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com