
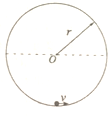
 如图所示,宇航员在地球表面完成以下实验:在固定的竖直光滑圆弧轨道内部的最低点,给质量为m的小球水平初速度v,小球恰能在竖直平面内做完整的圆周运动,而宇航员在某星球表面重复上述实验时发现小球只能上升至圆心等高处.已知该星球半径为地球半径的2倍,小球可视为质点,可求得该星球和地球的密度之比为( )
如图所示,宇航员在地球表面完成以下实验:在固定的竖直光滑圆弧轨道内部的最低点,给质量为m的小球水平初速度v,小球恰能在竖直平面内做完整的圆周运动,而宇航员在某星球表面重复上述实验时发现小球只能上升至圆心等高处.已知该星球半径为地球半径的2倍,小球可视为质点,可求得该星球和地球的密度之比为( )| A. | 5:4 | B. | 4:5 | C. | 5:1 | D. | 1:5 |
分析 在地球表面,根据牛顿第二定律求出最高点的速度,结合动能定理求出求出地球表面的重力加速度,根据动能定理求出星球表面的重力加速度,从而得出重力加速度的比值.根据万有引力等于重力得出星球质量的表达式,结合密度公式求出星球密度的表达式,抓住重力加速度和星球半径之比求出密度之比.
解答 解:在地球表面,小球恰能在竖直平面内做完整的圆周运动,在最高点有:$m{g}_{1}=m\frac{{{v}_{1}}^{2}}{r}$,解得${v}_{1}=\sqrt{{g}_{1}r}$.
根据动能定理得,$m{g}_{1}•2r=\frac{1}{2}m{v}^{2}-\frac{1}{2}m{{v}_{1}}^{2}$,解得g1=$\frac{{v}^{2}}{5r}$.
在星球的表面,小球只能上升至圆心等高处,根据动能定理得,$m{g}_{2}r=\frac{1}{2}m{v}^{2}$,解得${g}_{2}=\frac{{v}^{2}}{2r}$,
则$\frac{{g}_{1}}{{g}_{2}}=\frac{2}{5}$,
根据$G\frac{Mm}{{R}^{2}}=mg$得,质量M=$\frac{g{R}^{2}}{G}$,则密度$ρ=\frac{M}{\frac{4π{R}^{3}}{3}}$=$\frac{3g}{4πGR}$,
因为星球表面的重力加速度与地球表面重力加速度的比值为5:2,半径之比为2:1,则密度之比为5:4.
故选:A.
点评 本题考查了动能定理、牛顿第二定律和万有引力定律的综合运用,通过牛顿第二定律和动能定理求出星球和地球表面的重力加速度之比是解决本题的关键.


科目:高中物理 来源: 题型:选择题
 如图所示,粗细均匀竖直放置的玻璃管中,P为一小活塞,有一段水银柱将封闭在玻璃管中的空气分成上、下两部分,活塞和水银柱都静止不动.现在用力向下压活塞,使得活塞向下移动一段距离L,同时水银柱将向下缓慢移动一段距离为H,其中温度不变,则有( )
如图所示,粗细均匀竖直放置的玻璃管中,P为一小活塞,有一段水银柱将封闭在玻璃管中的空气分成上、下两部分,活塞和水银柱都静止不动.现在用力向下压活塞,使得活塞向下移动一段距离L,同时水银柱将向下缓慢移动一段距离为H,其中温度不变,则有( )| A. | L>H | B. | L<H | C. | L=H | D. | 无法判断 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,水平地面上固定一绝缘光滑长方体abcd-a′b′c′d′,长ab为15m,宽ad为10m,高aa′为5m,MN、PQ与ad相互平行,且aN、NQ、Qb间距离都为5m.一个半径为R=5m的$\frac{1}{4}$圆弧的光滑绝缘轨道被竖直固定,圆弧轨道的最高点E与它的圆心O在同一水平线上,M为该装置与cd的切点,区域MNQP、PQbc存在竖直方向的匀强磁场,磁感应强度大小分别为B1=1T和B2=2T,方向相反,边界MN、PQ处无磁场.从E点静止释放一质量m1=0.1kg,带正电荷q=0.1C的小球.g=10m/s2.求:
如图所示,水平地面上固定一绝缘光滑长方体abcd-a′b′c′d′,长ab为15m,宽ad为10m,高aa′为5m,MN、PQ与ad相互平行,且aN、NQ、Qb间距离都为5m.一个半径为R=5m的$\frac{1}{4}$圆弧的光滑绝缘轨道被竖直固定,圆弧轨道的最高点E与它的圆心O在同一水平线上,M为该装置与cd的切点,区域MNQP、PQbc存在竖直方向的匀强磁场,磁感应强度大小分别为B1=1T和B2=2T,方向相反,边界MN、PQ处无磁场.从E点静止释放一质量m1=0.1kg,带正电荷q=0.1C的小球.g=10m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
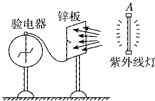 如图所示,一验电器与锌板相连,在A处用一紫外线灯照射锌板,关灯后,指针保持一定偏角.此时锌板带正电.(填“正”或“负”).使验电器指针回到零,再用相同强度的钠灯发出的黄光照射锌板,验电器指针无偏转.那么,若改用强度更大的红外线灯照射锌板,可观察到验电器指针无(填“有”或“无”)偏转.
如图所示,一验电器与锌板相连,在A处用一紫外线灯照射锌板,关灯后,指针保持一定偏角.此时锌板带正电.(填“正”或“负”).使验电器指针回到零,再用相同强度的钠灯发出的黄光照射锌板,验电器指针无偏转.那么,若改用强度更大的红外线灯照射锌板,可观察到验电器指针无(填“有”或“无”)偏转.查看答案和解析>>
科目:高中物理 来源: 题型:实验题
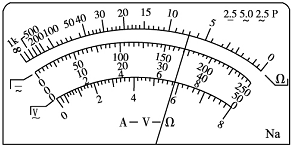
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,左端封闭右端开口的细玻璃管水平放置,用h=20cm水银柱封闭了长为L=65cm理想气体,水银柱右端距玻璃管开口端l=10cm.已知外界大气压强p0=76cmHg,温度t=27℃,重力加速度g=9.8m/s2.求:
如图所示,左端封闭右端开口的细玻璃管水平放置,用h=20cm水银柱封闭了长为L=65cm理想气体,水银柱右端距玻璃管开口端l=10cm.已知外界大气压强p0=76cmHg,温度t=27℃,重力加速度g=9.8m/s2.求:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:实验题
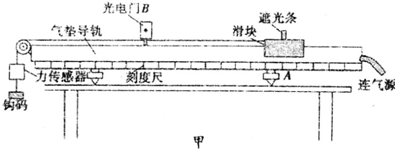
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com