
| gR |
| 1 |
| 2 |
| (2+μ)mg |
| cosθ+μsinθ |
| 1 |
| 2 |
| 1 |
| 2 |
| 8gR |
| v12 |
| R |
| mv1 |
| Bl |
. |
| I |
| ||
| r |
. |
| E |
| △Φ |
| △t |
| Blx |
| △t |
. |
| I |
| Blx |
| r |
mr
| ||
| B2l2 |
| (2+μ)mg |
| cosθ+μsinθ |
mr
| ||
| B2l2 |


 期末集结号系列答案
期末集结号系列答案科目:高中物理 来源: 题型:阅读理解
| gR |

查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解
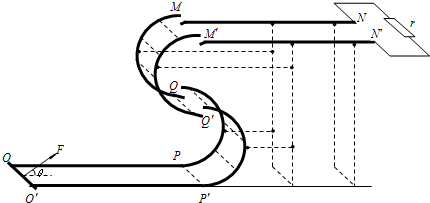
如图所示,固定在上、下两层水平面上的平行金属导轨![]() 、
、![]() 和
和![]() 、
、![]() 间距都是
间距都是![]() ,二者之间固定有两组竖直半圆形轨道
,二者之间固定有两组竖直半圆形轨道![]() 和
和![]() ,两轨道间距也均为
,两轨道间距也均为![]() ,且
,且![]() 和
和![]() 的竖直高度均为4R,两组半圆形轨道的半径均为R。轨道的
的竖直高度均为4R,两组半圆形轨道的半径均为R。轨道的![]() 端、
端、![]() 端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为
端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为![]() 的金属杆沿垂直导轨方向放在下层导轨的最左端
的金属杆沿垂直导轨方向放在下层导轨的最左端![]() 位置,金属杆在与水平成
位置,金属杆在与水平成![]() 角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端
角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端![]() 位置时其速度大小
位置时其速度大小![]() 。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
(1)已知金属杆与下层导轨间的动摩擦因数为![]() ,求金属杆所受恒力F的大小;
,求金属杆所受恒力F的大小;
(2)金属杆运动到![]() 位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道
位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道![]() 和
和![]() ,又在对接狭缝
,又在对接狭缝![]() 和
和![]() 处无碰撞地水平进入第二组半圆形轨道
处无碰撞地水平进入第二组半圆形轨道![]() 和
和![]() 的内
的内
侧,求金属杆运动到半圆轨道的最高位置![]() 时,它对轨道作用力的大小;
时,它对轨道作用力的大小;
(3)若上层水平导轨足够长,其右端连接的定值电阻阻值为![]() ,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置
,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置![]() 处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行。求金属杆在上层导轨上滑行的最大距离。
处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行。求金属杆在上层导轨上滑行的最大距离。
查看答案和解析>>
科目:高中物理 来源: 题型:阅读理解
(20分)如图所示,固定在上、下两层水平面上的平行金属导轨、
和
、
间距都是
,二者之间固定有两组竖直半圆形轨道
和
,两轨道间距也均为
,且
和
的竖直高度均为4R,两组半圆形轨道的半径均为R。轨道的
端、
端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为
的金属杆沿垂直导轨方向放在下层导轨的最左端
位置,金属杆在与水平成
角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端
位置时其速度大小
。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
(1)已知金属杆与下层导轨间的动摩擦因数为,求金属杆所受恒力F的大小;
(2)金属杆运动到位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道
和
,又在对接狭缝
和
处无碰撞地水平进入第二组半圆形轨道
和
的内
侧,求金属杆运动到半圆轨道的最高位置时,它对轨道作用力的大小;
(3)若上层水平导轨足够长,其右端连接的定值电阻阻值为,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置
处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行。求金属杆在上层导轨上滑行的最大距离。
查看答案和解析>>
科目:高中物理 来源:2010年甘肃省高三5月月考(理综)生物部分 题型:计算题
(20分)如图所示,固定在上、下两层水平面上的平行金属导轨 、
、 和
和 、
、 间距都是
间距都是 ,二者之间固定有两组竖直半圆形轨道
,二者之间固定有两组竖直半圆形轨道 和
和 ,两轨道间距也均为
,两轨道间距也均为 ,且
,且 和
和 的竖直高度均为4R,两组半圆形轨道的半径均为R。轨道的
的竖直高度均为4R,两组半圆形轨道的半径均为R。轨道的 端、
端、 端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为
端的对接狭缝宽度可忽略不计,图中的虚线为绝缘材料制成的固定支架,能使导轨系统位置固定。将一质量为 的金属杆沿垂直导轨方向放在下层导轨的最左端
的金属杆沿垂直导轨方向放在下层导轨的最左端 位置,金属杆在与水平成
位置,金属杆在与水平成 角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端
角斜向上的恒力作用下沿导轨运动,运动过程中金属杆始终与导轨垂直,且接触良好。当金属杆通过4R的距离运动到导轨末端 位置时其速度大小
位置时其速度大小 。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
。金属杆和导轨的电阻、金属杆在半圆轨道和上层水平导轨上运动过程中所受的摩擦阻力,以及整个运动过程中所受空气阻力均可忽略不计。
(1)已知金属杆与下层导轨间的动摩擦因数为 ,求金属杆所受恒力F的大小;
,求金属杆所受恒力F的大小;
(2)金属杆运动到 位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道
位置时撤去恒力F,金属杆将无碰撞地水平进入第一组半圆轨道 和
和 ,又在对接狭缝
,又在对接狭缝 和
和 处无碰撞地水平进入第二组半圆形轨道
处无碰撞地水平进入第二组半圆形轨道 和
和 的内
的内
侧,求金属杆运动到半圆轨道的最高位置 时,它对轨道作用力的大小;
时,它对轨道作用力的大小;
(3)若上层水平导轨足够长,其右端连接的定值电阻阻值为 ,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置
,导轨处于磁感应强度为B、方向竖直向下的匀强磁场中。金属杆由第二组半圆轨道的最高位置 处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行。求金属杆在上层导轨上滑行的最大距离。
处,无碰撞地水平进入上层导轨后,能沿上层导轨滑行。求金属杆在上层导轨上滑行的最大距离。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com