
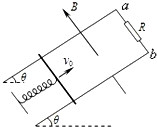
 如图所示,固定的光滑金属导轨间距为L,导轨电阻不计,上端a、b间接有阻值为R的电阻,导轨平面与水平面的夹角为θ,且处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中.质量为m、有效阻值为$\frac{R}{2}$导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行.求:
如图所示,固定的光滑金属导轨间距为L,导轨电阻不计,上端a、b间接有阻值为R的电阻,导轨平面与水平面的夹角为θ,且处在磁感应强度大小为B、方向垂直于导轨平面向上的匀强磁场中.质量为m、有效阻值为$\frac{R}{2}$导体棒与固定弹簧相连后放在导轨上.初始时刻,弹簧恰处于自然长度,导体棒具有沿轨道向上的初速度v0.整个运动过程中导体棒始终与导轨垂直并保持良好接触.已知弹簧的劲度系数为k,弹簧的中心轴线与导轨平行.求:分析 (1)棒向上运动切割磁感线,由E1=BLv0求感应电动势,由欧姆定律求感应电流,根据右手定则判断感应电流的方向;
(2)当导体棒第一次回到初始位置时,速度变为v,棒产生的感应电动势为E2=BLv,再由欧姆定律求得感应电流,由F=BIL求出此时棒所受的安培力,根据牛顿第二定律就可以求出加速度;
(3)导体棒最终静止时,由胡克定律求出弹簧的被压缩长度x,对整个过程,运用能量守恒列式,可求出回路产生的总热量,再串联关系求出R上产生的焦耳热Q.
解答 解: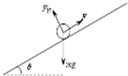 (1)棒产生的感应电动势为:E1=BLv0
(1)棒产生的感应电动势为:E1=BLv0
通过R的电流大小为:${I}_{1}=\frac{{E}_{1}}{R+\frac{R}{2}}$=$\frac{2BL{v}_{0}}{3R}$
根据右手定则判断得知:电流方向为:b→a
(2)棒产生的感应电动势为:E2=BLv
感应电流为:${I}_{2}=\frac{{E}_{2}}{R+\frac{R}{2}}$
棒受到的安培力大小为:$F=BIL=\frac{{B}^{2}{L}^{2}v}{R+\frac{1}{2}R}$=$\frac{{2B}^{2}{L}^{2}v}{3R}$,方向沿斜面向上,如图所示.
根据牛顿第二定律 有:mgsinθ-F=ma
解得:$a=gsinθ-\frac{{2B}^{2}{L}^{2}v}{3mR}$
(3)导体棒最终静止,:mgsinθ=kx
弹簧的压缩量为:$x=\frac{mgsinθ}{k}$
设整个过程回路产生的焦耳热为Q0,根据能量守恒定律,有:
$\frac{1}{2}m{{v}_{0}}^{2}+mgxsinθ={E}_{P}+{Q}_{0}$
解得:${Q}_{0}=\frac{1}{2}m{{v}_{0}}^{2}+\frac{(mgsinθ)^{2}}{k}-{E}_{P}$
电阻R上产生的焦耳热为:
$Q=\frac{R}{R+\frac{1}{2}R}{Q}_{0}=\frac{2}{3}[\frac{1}{2}m{{v}_{0}}^{2}+\frac{{(mgsinθ)}^{2}}{k}-{E}_{P}]$
答:(1)初始时刻通过电阻R的电流I的大小为$\frac{2BL{v}_{0}}{3R}$,方向为b→a;
(2)此时导体棒的加速度大小a为$gsinθ-\frac{{2B}^{2}{L}^{2}v}{3mR}$;
(3)导体棒从开始运动直到停止的过程中,电阻R上产生的焦耳热Q为$\frac{2}{3}[\frac{1}{2}m{{v}_{0}}^{2}+\frac{{(mgsinθ)}^{2}}{k}-{E}_{P}]$.
点评 本题是导体棒在导轨上滑动的类型,分析、计算安培力和分析能量如何转化是解题的关键,综合性较强.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
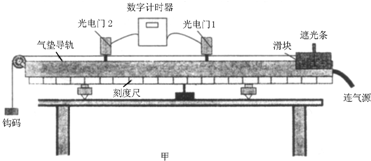
| 实验序号 | 滑块质量m/g | 滑块加速度a/m•s-2 |
| 1 | 250 | 1.80 |
| 2 | 300 | 1.50 |
| 3 | 350 | 1.29 |
| 4 | 400 | 1.13 |
| 5 | 500 | 0.90 |
| 6 | 800 | 0.56 |
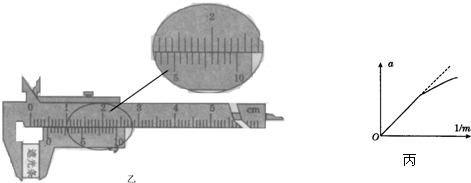
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
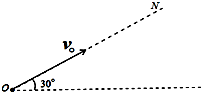 如图所示,质量为m、电量为q的小球在电场强度E的匀强电场中,以初速度v0沿直线ON做匀变速运动,直线ON与水平面的夹角为30°,若小球在初始位置的电势能为零,重力加速度为g,且mg=qE,则下面说法中正确的是( )
如图所示,质量为m、电量为q的小球在电场强度E的匀强电场中,以初速度v0沿直线ON做匀变速运动,直线ON与水平面的夹角为30°,若小球在初始位置的电势能为零,重力加速度为g,且mg=qE,则下面说法中正确的是( )| A. | 电场方向竖直向上 | B. | 小球运动的加速度大小为g | ||
| C. | 小球最大高度为$\frac{V_0^2}{2g}$ | D. | 小球电势能的最大值为$\frac{mV_0^2}{2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
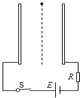 如图所示,足够长的两平行金属板正对着竖直放置,它们通过导线与电源E、定值电阻R、开关S相连.闭合开关后,一个带电的液滴从两板上端的中点处无初速度释放,最终液滴落在某一金属板上.下列说法中正确的是( )
如图所示,足够长的两平行金属板正对着竖直放置,它们通过导线与电源E、定值电阻R、开关S相连.闭合开关后,一个带电的液滴从两板上端的中点处无初速度释放,最终液滴落在某一金属板上.下列说法中正确的是( )| A. | 电源电动势越大,液滴在板间运动的加速度越大 | |
| B. | 定值电阻的阻值越小,液滴在板间运动的加速度越大 | |
| C. | 定值电阻的阻值越大,液滴在板间运动的时间越长 | |
| D. | 两平行金属板距离越大,液滴在板间运动的时间越长 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
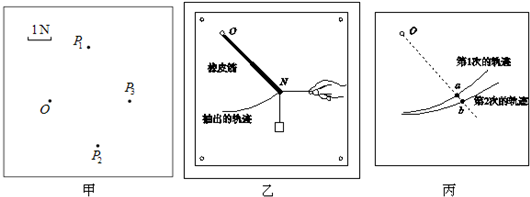
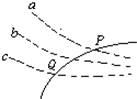 图中虚线a、b、c代表电场中的三条等势线,相邻两等势线之间的电势差相等,实线为一带正电的微粒仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,P、Q相比( )
图中虚线a、b、c代表电场中的三条等势线,相邻两等势线之间的电势差相等,实线为一带正电的微粒仅在电场力作用下通过该区域时的运动轨迹,P、Q是这条轨迹上的两点,P、Q相比( )| A. | Q点的电势比P点的高 | B. | 带电微粒在P点时的电势能较大 | ||
| C. | 带电微粒通过P点时动能较大 | D. | 带电微粒通过Q点时的加速度较大 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 速度逐渐减小,当加速度减小到零时,速度达到最小值 | |
| B. | 速度逐渐增大,当加速度减小到零时,速度达到最大值 | |
| C. | 位移逐渐增大,当加速度减小到零时,位移将还要增大 | |
| D. | 位移逐渐减小,当加速度减小到零时,位移将不再减少 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com