
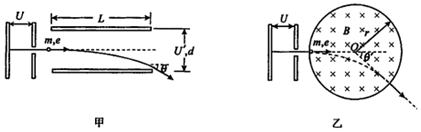
分析 (1)a.分析可知粒子在加速场中做加速运动,运用动能定理即可求出粒子的速度,进入偏转电场后粒子做类平抛运动,运用运动的合成和分解结合牛顿第二定律以及速度偏转角公式,联立即可求出偏转角θ的正切值;
b.加速过程与a问中相同,进入磁场后做匀速圆周运动,洛伦兹力提供向心力结合几何关系,求出含θ′的表达式,改变表达式中的参量,即可找出使增大偏转角θ′的方法;
(2)建立围观模型,通过电流的微观表达式I=nqSv,找到q和I之间的关系,即可证明两个定义式的一致性.
解答 解:(1)a.在加速电场中,由动能定理可得:eU=$\frac{1}{2}m{v}^{2}$
解得:v=$\sqrt{\frac{2eU}{m}}$
在偏转电场中,电子做类平抛运动,设运动时间为t
有运动的分解可知:
水平方向:L=vt
竖直方向:vy=at,$\frac{U′}{d}e$=ma
速度偏转角正切值为:tanθ=$\frac{{v}_{y}}{v}$
解得:tanθ=$\frac{U′L}{2Ud}$
b.由a问可知,入射电场的速度:v=$\sqrt{\frac{2eU}{m}}$
在匀强磁场中,电子做匀速圆周运动,根据洛伦兹力提供向心力可得:
evB=m$\frac{{v}^{2}}{R}$
解得:R=$\sqrt{\frac{2Um}{e{B}^{2}}}$
电子在磁场中的运动轨迹如图所示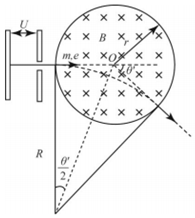
tan$\frac{θ′}{2}$=$\frac{r}{R}$
解得:tan$\frac{θ′}{2}$=r$\sqrt{\frac{e{B}^{2}}{2Um}}$
增大偏转角θ′即增大tan$\frac{θ′}{2}$,可采用的方法有:
增大磁场应强度B,增大匀强磁场半径r,减小加速电压U
(2)由洛伦兹力公式得:F洛=qvB可知,B=$\frac{{F}_{洛}}{qv}$
根据题意构建模型如下:
如图所示,在一匀强磁场中有一段固定的长为L的直导线,已知导线横截面积为S,
单位体积内自由电荷数为n,导线内自由电荷定向运动速率为v,磁场的磁感应强度为B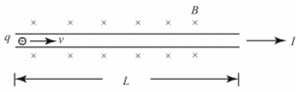
则导线内自由电荷数:N=nSL
安培力与洛伦兹力的关系为:F安=N•F洛,
导线内电流的微观表达式:I=nqSv,
联立上面三个式子可得:B=$\frac{{F}_{洛}}{qv}$=$\frac{{F}_{安}}{Nqv}$=$\frac{{F}_{安}}{qv•nSL}$=$\frac{{F}_{安}}{IL}$
即定义式:B=$\frac{{F}_{洛}}{qv}$与B=$\frac{{F}_{安}}{IL}$这一定义式是一致的.
答:(1)a.电子射入偏转电场时速度的大小v为$\sqrt{\frac{2eU}{m}}$,射出偏转电场时速度偏转角θ的正切值为$\frac{U′L}{2Ud}$;
b.增大偏转角θ′的方法:增大磁场应强度B,增大匀强磁场半径r,减小加速电压U;
(2)磁感应强度B的定义式为B=$\frac{{F}_{洛}}{qv}$,证明过程见解析.
点评 本题考查带电粒子在复合场中的运动,解题的关键是要正确画出粒子轨迹过程图,明确每一个过程粒子的运动性质,针对每一个过程选择合适的规律解决问题;第二问较难,要根据两个定义式中的物理量建立微观物理模型才能证明出两个定义式的一致性.


 黄冈创优卷系列答案
黄冈创优卷系列答案科目:高中物理 来源: 题型:填空题
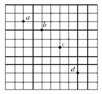 在研究平抛运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=1.25cm,若小球在平抛运动中的几个位置如图中的a、b、c、d所示,则小球的初速度的计算公式为v0=$2\sqrt{gL}$(用L、g表示),其值是0.7m/s(取g=9.8m/s2),经过d点时的速率v=$\frac{\sqrt{65gL}}{2}$(用L、g表示),起点到a的距离为$\frac{\sqrt{65}}{8}L$(用L、g表示).
在研究平抛运动的实验中,用一张印有小方格的纸记录轨迹,小方格的边长L=1.25cm,若小球在平抛运动中的几个位置如图中的a、b、c、d所示,则小球的初速度的计算公式为v0=$2\sqrt{gL}$(用L、g表示),其值是0.7m/s(取g=9.8m/s2),经过d点时的速率v=$\frac{\sqrt{65gL}}{2}$(用L、g表示),起点到a的距离为$\frac{\sqrt{65}}{8}L$(用L、g表示).查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 悬挂点在两边绳子的拉力作用下平衡 | |
| B. | 绷紧的晾衣绳无法受力 | |
| C. | 晾衣绳绷紧时受到的合力更大 | |
| D. | 合力相等时.分力间夹角越大分力越大 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | A、B两点的角速度相等 | B. | A、B两点的线速度相等 | ||
| C. | A、B两点的转动半径相同 | D. | A、B两点的转动加速度相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
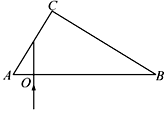 如图所示为一直角棱镜的截面图,∠ACB=90°,∠CAB=60°,AC边长为L.一平行细光束从AB面上的O点沿垂直于AB面的方向射入棱镜,经AC面的中点 P反射后,在BC面上的M点同时发生反射和折射,且反射光线和折射光线互相垂直(P点和M点图中未画出),反射光线从AB面的O'射出,已知光在真空中的传播速度为c,求:
如图所示为一直角棱镜的截面图,∠ACB=90°,∠CAB=60°,AC边长为L.一平行细光束从AB面上的O点沿垂直于AB面的方向射入棱镜,经AC面的中点 P反射后,在BC面上的M点同时发生反射和折射,且反射光线和折射光线互相垂直(P点和M点图中未画出),反射光线从AB面的O'射出,已知光在真空中的传播速度为c,求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
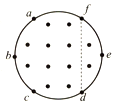 如图所示,abcdef为圆形磁场区域的圆周上的6个等分点,比荷相同的粒子先后从f沿fd方向射入磁场区域.从a点离开磁场的粒子,速度大小为va,在磁场中运动的时间为ta,从c点离开磁场的粒子,速度大小为vc,在磁场中运动的时间为tc,不计粒子重力,则( )
如图所示,abcdef为圆形磁场区域的圆周上的6个等分点,比荷相同的粒子先后从f沿fd方向射入磁场区域.从a点离开磁场的粒子,速度大小为va,在磁场中运动的时间为ta,从c点离开磁场的粒子,速度大小为vc,在磁场中运动的时间为tc,不计粒子重力,则( )| A. | $\frac{{v}_{a}}{{v}_{c}}$=$\frac{1}{4}$,$\frac{{t}_{a}}{{t}_{c}}$=$\frac{3}{1}$ | B. | $\frac{{v}_{a}}{{v}_{c}}$=$\frac{1}{4}$,$\frac{{t}_{a}}{{t}_{c}}$=$\frac{2}{1}$ | ||
| C. | $\frac{{v}_{a}}{{v}_{c}}$=$\frac{1}{2}$,$\frac{{t}_{a}}{{t}_{c}}$=$\frac{2}{1}$ | D. | $\frac{{v}_{a}}{{v}_{c}}$=$\frac{1}{2}$,$\frac{{t}_{a}}{{t}_{c}}$=$\frac{3}{1}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
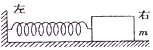 如图所示,物块的质量为m,它与水平桌面间的动摩擦因数为μ.起初,用手按住物块,物块的速度为零,弹簧的伸长量为x.然后放手,当弹簧第一次恢复原长时,物块的速度为v.则此过程中弹力所做的功为( )
如图所示,物块的质量为m,它与水平桌面间的动摩擦因数为μ.起初,用手按住物块,物块的速度为零,弹簧的伸长量为x.然后放手,当弹簧第一次恢复原长时,物块的速度为v.则此过程中弹力所做的功为( )| A. | $\frac{1}{2}$mv2+μmgx | B. | $\frac{1}{2}$mv2-μmgx | C. | μmgx-$\frac{1}{2}$mv2 | D. | 以上选项均不对 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
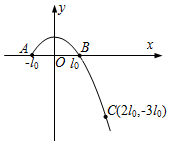 如图所示,在xOy平面内,将质量为m的小物体(可看成质点)以一定速度从A点斜向上抛出,B和C是粒子运动轨迹上的两点,如图所示,其中l0为常数,忽略空气阻力,求:
如图所示,在xOy平面内,将质量为m的小物体(可看成质点)以一定速度从A点斜向上抛出,B和C是粒子运动轨迹上的两点,如图所示,其中l0为常数,忽略空气阻力,求:查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 速度等于0 | B. | 速度等于$\sqrt{Rg}$ | ||
| C. | 小球对轨道压力等于mg | D. | 小球对轨道压力等于0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com