
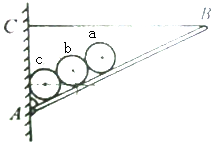
 有一轻质木板AB长为L,A端用铰链固定在竖直墙上,另一端用水平轻绳CB拉住.板上依次放着a、b、c三个圆柱体,半径均为r,重均为G,木板与墙的夹角为θ,如图所示,不计一切摩擦,求BC绳上的张力.
有一轻质木板AB长为L,A端用铰链固定在竖直墙上,另一端用水平轻绳CB拉住.板上依次放着a、b、c三个圆柱体,半径均为r,重均为G,木板与墙的夹角为θ,如图所示,不计一切摩擦,求BC绳上的张力. 分析 依次对圆柱体a、b、c进行受力分析,由共点力的平衡求出它们对杆AB的压力;最好以AB杆为研究的对象,受力分析,并找出各个力的力矩,在由力矩平衡的条件得出BC的拉力.
解答 解:以圆柱体a为研究的对象,a受到重力、杆的支持力和b的支持力,受力如图1,则:
Na=G•cosθ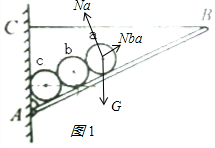
Nba=Gsinθ
以圆柱体b为研究的对象,b受到重力、杆的支持力、a对b的压力,以及c对b的支持力,受力如图2,则:
Nb=Gcosθ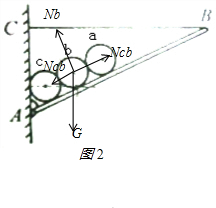
Ncb=Nab+Gsinθ
由牛顿第三定律得:Nab=Nba
所以:Ncb=2Gsinθ
以圆柱体b为研究的对象,b受到重力、杆的支持力、a对b的压力,以及c对b的支持力,奖受到的力沿斜面方向与垂直于斜面的方向分解,受力如图3,则:
由牛顿第三定律得:Nbc=Ncb=2Gsinθ
沿x方向:N1cosθ=Gsinθ+Nbc
沿y方向:Nc=Gcosθ+N1sinθ
联立以上三式得:Nc=Gcosθ+3Gsinθ•tanθ
以杆AB为研究对象,杆的重力不计,杆受到abc三个圆柱体的压力与绳子BC的拉力,根据牛顿第三定律可知,圆柱体对杆的压力大小等于杆对圆柱体的支持力,各拉力相对于支点A的力臂如图4,根据力矩平衡的条件得: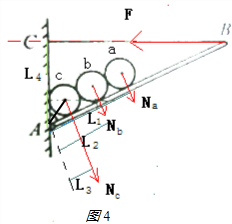
FL4=NaL1+NbL2+NcL3
其中:${L}_{3}=\frac{r}{sin\frac{θ}{2}}$,L2=L3+2r,L1=L2+2r,${L}_{4}=\overline{AB}•cosθ=L•cosθ$
联立方程,整理得:
$F=\frac{3G}{L}•(\frac{r}{sin\frac{θ}{2}}+2r+\frac{r}{sin\frac{θ}{2}}•\frac{si{n}^{2}θ}{co{s}^{2}θ})$
答:BC绳上的张力是$\frac{3G}{L}•(\frac{r}{sin\frac{θ}{2}}+2r+\frac{r}{sin\frac{θ}{2}}•\frac{si{n}^{2}θ}{co{s}^{2}θ})$
点评 该题中由于abc三个圆柱体对杆AB的作用点不在同一点,要分别求出圆柱体abc受到的支持力,然后才能使用力矩平衡的条件来解题.题目的思路比较简单,就是解答的步骤太多太复杂.


 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案科目:高中物理 来源: 题型:解答题
 在图所示的电路中,L为标有“6V 3W”的小灯泡,电源的内电阻r=2Ω,滑动变阻器的滑动片触头位于变阻器的中点时,灯泡L恰好能正常发光,这时电压表的读数为27V,其中滑动变阻器的电阻为48Ω.求:
在图所示的电路中,L为标有“6V 3W”的小灯泡,电源的内电阻r=2Ω,滑动变阻器的滑动片触头位于变阻器的中点时,灯泡L恰好能正常发光,这时电压表的读数为27V,其中滑动变阻器的电阻为48Ω.求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
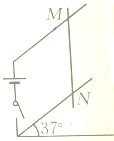 如图所示,电源、开关与光滑的金属导轨相连,导轨与水平方向成37°角放置,当导线MN放于导轨上时接通电源,通过MN的电流可达5A,把整个装置放在竖直方向的匀强磁场中,则MN刚好静止,试确定磁场的大小与方向.(MN的质量为10g,长为20m)
如图所示,电源、开关与光滑的金属导轨相连,导轨与水平方向成37°角放置,当导线MN放于导轨上时接通电源,通过MN的电流可达5A,把整个装置放在竖直方向的匀强磁场中,则MN刚好静止,试确定磁场的大小与方向.(MN的质量为10g,长为20m)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
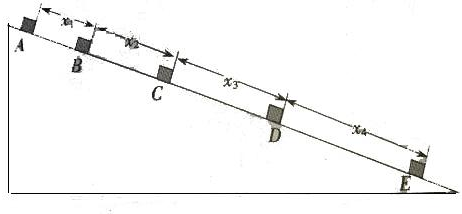
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
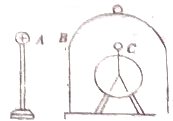 如图所示,放在绝缘台上的金属网罩内放有不带电的验电器C,若把一带有正电荷的绝缘体A移近金属网罩B,则( )
如图所示,放在绝缘台上的金属网罩内放有不带电的验电器C,若把一带有正电荷的绝缘体A移近金属网罩B,则( )| A. | 在B的内表面带正电荷,φB-φC=0 | B. | 在B的右侧外表面带正电荷 | ||
| C. | 验电器的金箔将张开,φB<φC | D. | B的左右两侧电势相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 安徽“淮南之眼”摩天轮是亚洲最高的山体摩天轮,如图所示,一质量为m的乘客坐在摩天轮中以速率v,在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻乘客在轨迹最低点且重力势能为零,那么,乘客运动过程中( )
安徽“淮南之眼”摩天轮是亚洲最高的山体摩天轮,如图所示,一质量为m的乘客坐在摩天轮中以速率v,在竖直平面内做半径为R的匀速圆周运动,假设t=0时刻乘客在轨迹最低点且重力势能为零,那么,乘客运动过程中( )| A. | 重力势能随时间的变化关系为Ep=mgRcos$\frac{v}{R}$t | |
| B. | 在最高点受到座位的支持力为m$\frac{{v}^{2}}{R}$-mg | |
| C. | 机械能守恒且为E=$\frac{1}{2}$mv2 | |
| D. | 机械能随时间的变化关系为E=$\frac{1}{2}$mv2+mgR(1-cos$\frac{v}{R}$t) |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
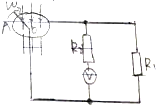 如图所示,在磁感应强度B=2T的匀强磁场中,有一个半径r=0.5m的金属圆环,圆环所在的平面与磁感线垂直,OA是一个金属棒,它沿着顺时针方向以12rad/s的角速度绕圆心O匀速运动,A端始终与圆环相接触OA棒的电阻R=1.0Ω,图中定值电阻R1=5Ω,R2=20Ω,电压表为理想电压表,圆环和连接导线的电阻忽略不计,求理想电压表的读数.
如图所示,在磁感应强度B=2T的匀强磁场中,有一个半径r=0.5m的金属圆环,圆环所在的平面与磁感线垂直,OA是一个金属棒,它沿着顺时针方向以12rad/s的角速度绕圆心O匀速运动,A端始终与圆环相接触OA棒的电阻R=1.0Ω,图中定值电阻R1=5Ω,R2=20Ω,电压表为理想电压表,圆环和连接导线的电阻忽略不计,求理想电压表的读数.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 一辆质量为5000kg的汽车,其发动机额定功率为P=60kW,在水平公路上以最大速度行驶.不久,汽车保持额定功率驶上倾角为θ的较长斜坡路段(已知sinθ=0.2,cosθ=0.98),已知汽车与水平公路、汽车与斜坡间的动摩擦因素均为μ=0.1.问:
一辆质量为5000kg的汽车,其发动机额定功率为P=60kW,在水平公路上以最大速度行驶.不久,汽车保持额定功率驶上倾角为θ的较长斜坡路段(已知sinθ=0.2,cosθ=0.98),已知汽车与水平公路、汽车与斜坡间的动摩擦因素均为μ=0.1.问:查看答案和解析>>
科目:高中物理 来源: 题型:填空题
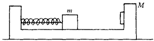 如图所示,质量为M的框架放在光滑的水平桌面上,质量为m的木块压缩着框架左侧的弹簧并用细线固定,木块距框架右侧为d.现在把线剪断,木块被弹簧推动,木块达到框架右侧并不弹回,木块与框架间的摩擦可以忽略不计.最后框架的位移为$\frac{md}{M+m}$.
如图所示,质量为M的框架放在光滑的水平桌面上,质量为m的木块压缩着框架左侧的弹簧并用细线固定,木块距框架右侧为d.现在把线剪断,木块被弹簧推动,木块达到框架右侧并不弹回,木块与框架间的摩擦可以忽略不计.最后框架的位移为$\frac{md}{M+m}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com