
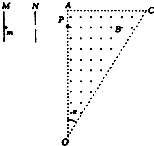
 如图所示,直角三角形OAC(a=30°)区域内有B=0.5T的匀强磁场,方向如图所示.两平行极板M、N接在电压为u的直流电源上,左板为高电势.一带正电的粒子从靠近M板由静止开始加速,从N板的小孔射出电场后,垂直OA的方向从P点进入磁场中.带电粒子的比荷为$\frac{q}{m}$=105C/kg,OP间距离为L=0.3m.全过程不计粒子所受的重力,则:
如图所示,直角三角形OAC(a=30°)区域内有B=0.5T的匀强磁场,方向如图所示.两平行极板M、N接在电压为u的直流电源上,左板为高电势.一带正电的粒子从靠近M板由静止开始加速,从N板的小孔射出电场后,垂直OA的方向从P点进入磁场中.带电粒子的比荷为$\frac{q}{m}$=105C/kg,OP间距离为L=0.3m.全过程不计粒子所受的重力,则:分析 (1)粒子在电场中直线加速,在磁场中做匀速圆周运动,临界情况是轨迹圆与OC边相切;从AO边射出时轨迹是半圆,结合推论公式T=$\frac{2πm}{qB}$和t=$\frac{θ}{2π}T$列式求解时间;
(2)粒子从OC边离开磁场时的最小电源电压U对应的轨迹是轨迹圆与OC边相切;最直线运动根据动能定理列式,对圆周运动根据牛顿第二定律列式,最后联立求解;
(3)根据公式t=$\frac{θ}{2π}T$,轨迹圆的圆心角最大时粒子在磁场中运动的时间最长,临界情况是轨迹圆与OC边相切.
解答 解:(1)带电粒子在磁场做圆周运动的周期为:
T=$\frac{2πm}{qB}$=$\frac{2π}{1{0}^{5}×0.5}$=4π×10-5s
当粒子从OA边射出时,粒子在磁场中恰好运动了半个周期:
t1=$\frac{T}{2}$=2π×10-5s
(2)当带电粒子的轨迹与OC边相切时为临界状态,如图所示:
结合几何关系,有:
R+$\frac{R}{sinα}$=L
解得:
R=0.1m
电荷被加速,则有:
$qU=\frac{1}{2}m{v}^{2}$
磁场中:
qvB=m$\frac{{v}^{2}}{R}$
联立解得:
U=$\frac{q{B}^{2}{R}^{2}}{2m}$=$\frac{1{0}^{5}×0.{5}^{2}×0.{1}^{2}}{2}$=125V
(3)粒子OC边边离开磁场,最大圆心角为120°,故粒子在磁场中运动的时间小于$\frac{1}{3}$周期,即:
$t<\frac{T}{3}$=$\frac{4π}{3}×1{0}^{-5}s$
答:(1)粒子从OA边离开磁场时粒子在磁场中运动的时间为2π×10-5s;
(2)粒子从OC边离开磁场时的最小电源电压U为125V;
(3)粒子OC边离开磁场时粒子在磁场中运动的最长时间为$\frac{4π}{3}×1{0}^{-5}s$.
点评 本题关键是明确粒子运动的运动性质,画出临界轨迹,然后结合动能定理和牛顿第二定律列式分析,不难.


 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中物理 来源: 题型:选择题
| A. | 30:31 | B. | 31:30 | C. | 1:2 | D. | 2:1 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,电源电动势为E0(未知),内阻不记,滑动变阻器的滑片P处于R的中点,一质量为m,带电荷量为q的粒子(重力不计)从加速电场AK当中的s3点由静止经加速电场加速后,沿s1s2方向从边长为L的正方形厂区的中间进入有界均匀场区,当场区内只加竖直向上的匀强电场(电场强度为E)时,带电粒子恰从b点射出场区.求电源的电动势E0.
如图所示,电源电动势为E0(未知),内阻不记,滑动变阻器的滑片P处于R的中点,一质量为m,带电荷量为q的粒子(重力不计)从加速电场AK当中的s3点由静止经加速电场加速后,沿s1s2方向从边长为L的正方形厂区的中间进入有界均匀场区,当场区内只加竖直向上的匀强电场(电场强度为E)时,带电粒子恰从b点射出场区.求电源的电动势E0.查看答案和解析>>
科目:高中物理 来源: 题型:填空题
 飞行衣是“特工”执行执行任务时的常用装备之一,主要由金属支架和高科技尼龙纤维组成,人穿上后展开双臂和双腿,看上去就像只蝙蝠,如图甲所示.某特工从悬停在空中的直升机上由静止跳下,距离直升机一段时间后打开飞行衣作减速下落,他打开飞行衣后的速度图线如图乙所示.这特工的质量为50kg,飞行衣的质量也为50kg,不记特工所受的阻力,打开飞行后飞行衣所受的阻力f与速度v成正比,即f=kv,(g取10m/s2)
飞行衣是“特工”执行执行任务时的常用装备之一,主要由金属支架和高科技尼龙纤维组成,人穿上后展开双臂和双腿,看上去就像只蝙蝠,如图甲所示.某特工从悬停在空中的直升机上由静止跳下,距离直升机一段时间后打开飞行衣作减速下落,他打开飞行衣后的速度图线如图乙所示.这特工的质量为50kg,飞行衣的质量也为50kg,不记特工所受的阻力,打开飞行后飞行衣所受的阻力f与速度v成正比,即f=kv,(g取10m/s2)查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图所示,重力为G的小球套在固定在竖直面内的半径为R的光滑的大圆环上,劲度为k的轻弹簧上端固定在大圆环的最高点,下端与小球相连,当小球静止时,弹簧处于伸长状态,与竖直方向间的夹角为θ=30°求
如图所示,重力为G的小球套在固定在竖直面内的半径为R的光滑的大圆环上,劲度为k的轻弹簧上端固定在大圆环的最高点,下端与小球相连,当小球静止时,弹簧处于伸长状态,与竖直方向间的夹角为θ=30°求查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
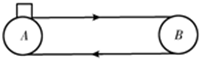 如图所示,水平传送带A、B两端点相距x=3.5m,以v0=2m/s的速度(始终保持不变)顺时针运转.今将一小煤块(可视为质点)无初速度地轻放在A点处,已知小煤块与传送带间的动摩擦因数为0.4.由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕.小煤块从A运动到B的过程中( )
如图所示,水平传送带A、B两端点相距x=3.5m,以v0=2m/s的速度(始终保持不变)顺时针运转.今将一小煤块(可视为质点)无初速度地轻放在A点处,已知小煤块与传送带间的动摩擦因数为0.4.由于小煤块与传送带之间有相对滑动,会在传送带上留下划痕.小煤块从A运动到B的过程中( )| A. | 煤块用了1s赶上皮带的速度 | |
| B. | 煤块从A处到B处所用的时间是2s | |
| C. | 划痕长度是4m | |
| D. | 煤块在静摩擦力作用下先做匀加速直线运动,再做匀速运动 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | a球获得的冲量最大 | |
| B. | b球损失的动能最多 | |
| C. | c球克服阻力做的功最多 | |
| D. | 三种碰撞过程,系统动量都是守恒的 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com