
分析 (1)将加速度用速度和时间的变化量来表示,然后化简得到速度和时间的变化量关系式,再对其进行累加即可求解;
(2)将加速度用位移和时间的变化量来表示,然后化简得到位移和时间的变化量关系式,再对其进行累加即可求解.
解答 解:(1)加速度$a=\frac{△v}{△t}={a}_{0}-kt$,那么,△v=a0△t-kt△t=$a△t-\frac{1}{2}k△{t}^{2}$,所以,当t=t0时质点的速率$v={v}_{0}+{a}_{0}{t}_{0}-\frac{1}{2}k{{t}_{0}}^{2}$;
(2)加速度$a=\frac{△v}{△t}=\frac{△x}{△t}•\frac{△v}{△x}=\frac{v△v}{△x}=\frac{\frac{1}{2}△{v}^{2}}{△x}={a}_{0}+kx$,那么,$△{v}^{2}=2{a}_{0}△x+2kx△x=2{a}_{0}△x+k△{x}^{2}$,所以,当x=x0时质点的速率$v=\sqrt{{{v}_{0}}^{2}+2{a}_{0}{x}_{0}+k{{x}_{0}}^{2}}$;
答:(1)若其加速度随时间的变化关系为a=a0-kt,式中a0,k(k>0)均为常量,则当t=t0时(a≠0)质点的速率为${v}_{0}+{a}_{0}{t}_{0}-\frac{1}{2}k{{t}_{0}}^{2}$;
(2)若其加速度随位移的变化关系为a=a0+kx,式中a0,k(k>0)均为常量,则当x=x0时质点的速率为$\sqrt{{{v}_{0}}^{2}+2{a}_{0}{x}_{0}+k{{x}_{0}}^{2}}$.
点评 在变速运动的运动学问题上,我们要熟悉速度、加速度、位移互相之间的关系式,并能对其进行相互转化.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:实验题
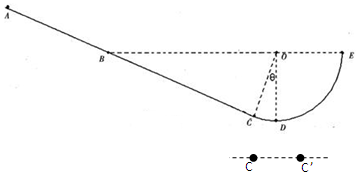
 如图所示,在《研究平抛物体的运动》的实验中,用一张印有小方格的纸记录轨迹,小方格的边长l=1×10-3m.若小球在平抛运动作图中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为vo=$2\sqrt{gl}$(用l、g表示),其值是0.2m/s(取g=10m/s2),小球在b点的速率是0.25m/s.
如图所示,在《研究平抛物体的运动》的实验中,用一张印有小方格的纸记录轨迹,小方格的边长l=1×10-3m.若小球在平抛运动作图中的几个位置如图中的a、b、c、d所示,则小球平抛的初速度的计算式为vo=$2\sqrt{gl}$(用l、g表示),其值是0.2m/s(取g=10m/s2),小球在b点的速率是0.25m/s.查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧栓接静止在水平面上,弹簧右端固定,质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B运动但与B不粘连.求:
如图所示,圆弧轨道与水平面平滑连接,轨道与水平面均光滑,质量为m的物块B与轻质弹簧栓接静止在水平面上,弹簧右端固定,质量为3m的物块A从圆弧轨道上距离水平面高h处由静止释放,与B碰撞后推着B运动但与B不粘连.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 40m | B. | 50m | C. | 32m | D. | 60m |
查看答案和解析>>
科目:高中物理 来源: 题型:实验题

查看答案和解析>>
科目:高中物理 来源: 题型:解答题
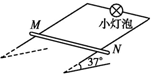 如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为1m,电阻忽略不计,其上端接一小灯泡,电阻为1Ω.一导体棒MN垂直于导轨放置,质量为0.5kg,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为1T.将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,求此后导体棒MN的运动速度以及小灯泡消耗的电功率(重力加速度g取10m/s2,sin 37°=0.6)
如图所示,足够长平行金属导轨倾斜放置,倾角为37°,宽度为1m,电阻忽略不计,其上端接一小灯泡,电阻为1Ω.一导体棒MN垂直于导轨放置,质量为0.5kg,接入电路的电阻为1Ω,两端与导轨接触良好,与导轨间的动摩擦因数为0.5.在导轨间存在着垂直于导轨平面的匀强磁场,磁感应强度为1T.将导体棒MN由静止释放,运动一段时间后,小灯泡稳定发光,求此后导体棒MN的运动速度以及小灯泡消耗的电功率(重力加速度g取10m/s2,sin 37°=0.6)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,在倾角为α的固定光滑斜面上,有一用绳子拴着的长木板,木板上站着一只猫.已知木板的质量是猫质量的3倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )
如图所示,在倾角为α的固定光滑斜面上,有一用绳子拴着的长木板,木板上站着一只猫.已知木板的质量是猫质量的3倍.当绳子突然断开时,猫立即沿着板向上跑,以保持其相对斜面的位置不变.则此时木板沿斜面下滑的加速度为( )| A. | $\frac{4g}{3}$sin α | B. | g sin α | C. | $\frac{3}{2}$g sin α | D. | 2g sin α |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
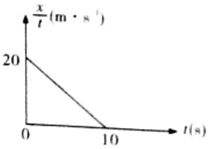
| A. | t=0时,物体初速度为10m/s | B. | 0~10s内物体运动方向未变 | ||
| C. | 0~10s内物体位移大小为0 | D. | 物体加速度大小为2m/s2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com