Question

7．高二某班做“用单摆测重力加速度”实验．
（1）在做“用单摆测定重力加速度”的实验中，以下做法正确的有AC
A．选用约1m长、不易形变的细线充当摆线
B．质量相同，体积不同的摆球，应选用体积较大的
C．单摆偏离平衡位置的角度不能过大，应控制在5°以内
D．当单摆经过平衡位置时开始计时，经过一次全振动后停止计时，用此时间间隔作为单摆的振动周期
（2）①用游标卡尺测量摆球直径d，把摆球用细线悬挂在铁架台上，用米尺测量出悬线长度l．
②在小钢球某次通过平衡位置时开始计时，并将这次通过平衡位置时记为0，数出以后小钢球通过平衡位置的次数为n，用停表记下所用的时间为t．请根据他的计数方法写出单摆周期的表达式：$\frac{2t}{n}$．
③用上面的测量数据计算重力加速度的表达式为g=$\frac{4{π}^{2}{n}^{2}（l+\frac{d}{2}）}{{t}^{2}}$．（用物理量l、d、n、t表达）
（3）某小组在利用单摆测定当地重力加速度的实验中如果测得g值偏小，原因可能是AC
A．把摆线长与小球直径之和做为摆长
B．摆线上端悬点未固定，振动中出现松动，使摆线长度增加了
C．开始计时时，秒表过迟按下
D．实验中误将49次全振动次数记为50次
（4）①根据某组在图中描出的点，请在图中描绘出T²-l图线；
②该组从图中求出图线斜率k，则重力加速度g与斜率k的关系式为g=$\frac{4{π}^{2}}{k}$；代入数据求得g=8.76m/s²（结果保留3位有效数字）．

Answer 1

分析 （1）单摆测定重力加速度的原理是：单摆的周期公式；在摆角很小的情况下，单摆的振动才是简谐运动；为减小空气阻力的影响，摆球的直径应远小于摆线的长度，选择密度较大的实心金属小球作为摆球．摆长等于摆线的长度加上摆球的半径．
（2）单摆完成一次全振动需要的时间是一个周期，应用单摆周期公式求出重力加速度的表达式．
（3）应用单摆周期公式求出重力加速度表达式，然后分析实验误差．
（4）应用单摆周期公式求出图象的函数表达式，然后根据函数表达式与图象分析答题．

解答 解：（1）A、为减小实验误差，摆长不能太短，选用约1m长、不易形变的细线充当摆线，故A正确；
B、为减小空气阻力对实验的影响，质量相同，体积不同的摆球，应选用体积较小的，故B错误；
C、在摆角很小的情况下，单摆的运动是简谐运动，单摆偏离平衡位置的角度不能过大，应控制在5°以内，故C正确；
D、为减小实验误差，测单摆周期时，应从单摆经过平衡位置时开始计时，测出多个周期的总时间然后求出平均值作为单摆的周期，故D错误；
（2）②单摆的周期：T=$\frac{t}{\frac{n}{2}}$=$\frac{2t}{n}$；
③由单摆的周期公式：T=2π$\sqrt{\frac{L}{g}}$可知，重力加速度：g=$\frac{4{π}^{2}L}{{T}^{2}}$=$\frac{4{π}^{2}（l+\frac{d}{2}）}{（\frac{t}{n}）^{2}}$=$\frac{4{π}^{2}{n}^{2}（l+\frac{d}{2}）}{{t}^{2}}$；
（3）由单摆的周期公式：T=2π$\sqrt{\frac{L}{g}}$可知，重力加速度：g=$\frac{4{π}^{2}L}{{T}^{2}}$；
A、把摆线长与小球直径之和做为摆长，摆长L偏大，由g=$\frac{4{π}^{2}L}{{T}^{2}}$可知，所测重力加速度g偏大，故A错误；
B、摆线上端悬点未固定，振动中出现松动，使摆线长度增加了，所测周期偏大，所测重力加速度偏小，故B正确；
C、开始计时时，秒表过迟按下，所测周期偏小，所测重力加速度偏大，故C错误；
D、实验中误将49次全振动次数记为50次，所测周期偏小，由g=$\frac{4{π}^{2}L}{{T}^{2}}$可知，所测重力加速度偏大，故D错误；故选B；
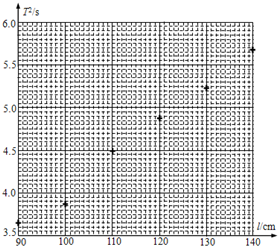
（4）①根据坐标系内描出的点作出图象如图所示：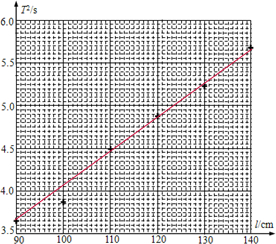

②由单摆的周期公式：T=2π$\sqrt{\frac{L}{g}}$可知，T²=$\frac{4{π}^{2}}{g}$L，T²-L图象的斜率：k=$\frac{4{π}^{2}}{g}$，则重力加速度：g=$\frac{4{π}^{2}}{k}$；
由图示图象可知，图象的斜率：k=$\frac{△{T}^{2}}{△l}$=$\frac{4.5-3.6}{1.10-0.90}$=4.5，则重力加速度：g=$\frac{4{π}^{2}}{k}$=$\frac{4×3.1{4}^{2}}{4.5}$≈8.76m/s²；
故答案为：（1）AC；（2）$\frac{2t}{n}$；$\frac{4{π}^{2}{n}^{2}（l+\frac{d}{2}）}{{t}^{2}}$；（3）B；（4）图象如图所示；$\frac{4{π}^{2}}{k}$；8.76．

点评 本题考查了用单摆测重力加速度实验，掌握实验原理、实验注意事项、应用单摆周期公式即可正确解题，本题难度不大，是一道基础题，学习时要注意基础知识的学习与掌握．