
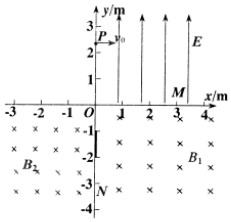
 如图所示,在平面直角坐标系xOy内,第一象限存在沿y轴正方向的匀强电场E,第四象限存在一匀强磁场B1,第三象限存在一匀强磁场B2,一带负电粒子,从y轴上一点p(0,$\frac{3\sqrt{3}}{2}$)沿x轴正方向射出,一段时间后经x轴上点M(3,0)进入第四象限,经点N(0,-3)穿过y轴,已知粒子在p点初速度v0=2×106m/s,粒子比荷$\frac{q}{m}$=3×106C/Kg,求:
如图所示,在平面直角坐标系xOy内,第一象限存在沿y轴正方向的匀强电场E,第四象限存在一匀强磁场B1,第三象限存在一匀强磁场B2,一带负电粒子,从y轴上一点p(0,$\frac{3\sqrt{3}}{2}$)沿x轴正方向射出,一段时间后经x轴上点M(3,0)进入第四象限,经点N(0,-3)穿过y轴,已知粒子在p点初速度v0=2×106m/s,粒子比荷$\frac{q}{m}$=3×106C/Kg,求:分析 (1)由类平抛运动的横向、纵向分位移联立求解即可;
(2)由(1)求得粒子在磁场中运动的速度及进入磁场时的方向,再根据圆弧的对称性及几何关系求得粒子运动的半径,进而由洛伦兹力作为向心力求得磁感应强度;
(3)由(2)的到粒子进入磁场的速度和方向,再根据几何关系求得弦长及半径,联立洛伦兹力作向心力即可求得磁感应强度.
解答 解:(1)粒子在第一象限内只受电场力作用,做类平抛运动,粒子运动加速度$a=\frac{F}{m}=\frac{q}{m}E$,
所以,根据类平抛运动的横向位移和纵向位移,有$\left\{\begin{array}{l}{3={v}_{0}t=2×1{0}^{6}t}\\{\frac{3\sqrt{3}}{2}=\frac{1}{2}a{t}^{2}=\frac{q}{2m}E{t}^{2}=\frac{3}{2}×1{0}^{6}E{t}^{2}}\end{array}\right.$;
所以,$E=\frac{\sqrt{3}×1{0}^{-6}}{{t}^{2}}=\frac{\sqrt{3}×1{0}^{-6}}{(\frac{3}{2}×1{0}^{-6})^{2}}=\frac{4\sqrt{3}}{9}×1{0}^{6}V/m$;
(2)粒子进入第四象限时的速度v可由(1)得:v的水平分量${v}_{x}={v}_{0}=2×1{0}^{6}m/s$,竖直分量${v}_{y}=\frac{qE}{m}t=3×1{0}^{6}×\frac{4\sqrt{3}}{9}×1{0}^{6}×\frac{3}{2×1{0}^{6}}m/s$=$2\sqrt{3}×1{0}^{6}m/s$,
所以,v=4×106m/s,v与x轴正方向成60°,所以,如下图所示,粒子在第四象限运动的圆心在l1上,连接MN,做MN的中垂线l2,
l1,l2的交点O′就是粒子在第四象限做圆周运动的圆心,由几何关系可知,粒子运动的半径$R=2×\frac{3}{1+\sqrt{3}}=3(\sqrt{3}-1)m$,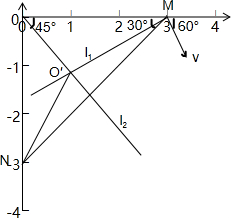
由粒子在第四象限中做圆周运动,洛伦兹力做向心力,所以有${B}_{1}vq=m\frac{{v}^{2}}{R}$,
所以,${B}_{1}=\frac{mv}{qR}=\frac{4×1{0}^{6}}{3×1{0}^{6}×3(\sqrt{3}-1)}=\frac{2}{9}(\sqrt{3}+1)T$;
(3)粒子在第三象限中只受洛伦兹力,做圆周运动,由圆弧的对称性可知,磁场边界y轴为一条直线,所以,粒子在第三象限运动轨迹的各圆弧相同,
因为挡板在-2≤y≤-1区域上,所以,粒子运动的弦长不小于1m,所以,粒子运动的弦长可谓3m,1.5m,1m;
设弦长为L,由(2)可知,O′N与y轴的夹角为30°,所以,如图所示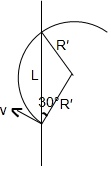
粒子在第三象限运动的半径$R′=\frac{\frac{L}{2}}{cos30°}=\frac{\sqrt{3}}{3}L$;
由洛伦兹力作向心力,可得:${B}_{2}vq=\frac{m{v}^{2}}{R′}$,
所以,${B}_{2}=\frac{mv}{qR′}=\frac{4×1{0}^{6}}{3×1{0}^{6}}×\frac{\sqrt{3}}{L}=\frac{4\sqrt{3}}{3}×\frac{1}{L}T$;
所以磁感应强度B2可能为$\frac{4\sqrt{3}}{9}T,\frac{8\sqrt{3}}{9}T,\frac{4\sqrt{3}}{3}T$.
答:(1)匀强电场的电场强度为$\frac{4\sqrt{3}}{9}×1{0}^{6}V/m$;
(2)匀强磁场B1的磁感应强度为$\frac{2}{9}(\sqrt{3}+1)T$;
(3)若y轴上在-2≤y≤-1区域有一弹性挡板,不考虑粒子与挡板碰撞的能量、比荷的变化,若要粒子从N点仅从第三象限运动到坐标原点O,则磁感应强度B2的可能值有$\frac{4\sqrt{3}}{9}T,\frac{8\sqrt{3}}{9}T,\frac{4\sqrt{3}}{3}T$.
点评 在求带电粒子在磁场中的运动问题时,要注意利用用几何关系,尤其是对称关系,求得粒子运动半径,在联立洛伦兹力作向心力来求解.


 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案 全优冲刺100分系列答案
全优冲刺100分系列答案科目:高中物理 来源: 题型:计算题
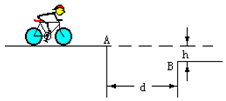 如图所示,骑车人欲穿过宽度d=4m的壕沟AB,现已知两沟沿的高度差h=0.8m.(g=10m/s2)求:
如图所示,骑车人欲穿过宽度d=4m的壕沟AB,现已知两沟沿的高度差h=0.8m.(g=10m/s2)求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 强相互作用力是原子核内部的力,弱相互作用力是原子核外部的力 | |
| B. | 强相互作用力和弱相互作用力都是短程力,其力程均在10-18米范围内 | |
| C. | 每个核子只跟邻近的核子发生核力作用,这种性质称为核力的饱和性 | |
| D. | 组成原子核的核子越多,它的结合能越低 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
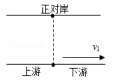 一条河两岸平行,河宽d=80m,河水流速v1=1m/s,一小船在静水中的速度为v2=2m/s.求:
一条河两岸平行,河宽d=80m,河水流速v1=1m/s,一小船在静水中的速度为v2=2m/s.求:查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 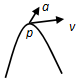 | B. | 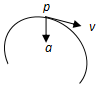 | ||
| C. | 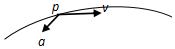 | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
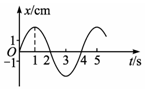 在水平方向上做简谐运动的质点,其振动图象如图所示.假设向右的方向为正方向,则物体加速度向右且速度向右的时间段是( )
在水平方向上做简谐运动的质点,其振动图象如图所示.假设向右的方向为正方向,则物体加速度向右且速度向右的时间段是( )| A. | 0 s到1 s内 | B. | 1 s到2 s内 | C. | 2 s到3 s内 | D. | 3 s到4 s内 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
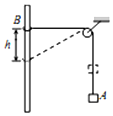 如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )
如图所示,物块A和圆环B用绕过定滑轮的轻绳连接在一起,圆环B套在光滑的竖直固定杆上,开始时连接B的绳子处于水平.零时刻由静止释放B,经时间t,B下降h,此时,速度达到最大.不计滑轮摩擦和空气的阻力,则( )| A. | t时刻B的速度大于A的速度 | |
| B. | t时刻B的加速度最大 | |
| C. | 0~t过程A的机械能增加量小于B的机械能减小量 | |
| D. | 0~t过程绳拉力对物块B做的功在数值上等于物块B机械能的减少量 |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 高度为H=2m圆柱形容器中盛满折射率n=$\sqrt{2}$的某种透明液体,容器直径L=3m,在圆心O点正上方h高度处有一点光源S.
高度为H=2m圆柱形容器中盛满折射率n=$\sqrt{2}$的某种透明液体,容器直径L=3m,在圆心O点正上方h高度处有一点光源S.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
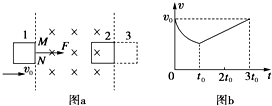
| A. | t=0时,线框右侧边MN的两端电压为Bav0 | |
| B. | 在t0时刻线框的速度为${v_0}-\frac{{F{t_0}}}{m}$ | |
| C. | 线框完全离开磁场的瞬间(位置3)的速度一定比t0时刻线框的速度大 | |
| D. | 线框从进入磁场(位置1)到完全离开磁场(位置3)的过程中产生的电热为2Fb |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com