练习册

  • 练习册
  • 试题
    精英家教网 > 高中物理 > 题目详情
    8．下列说法，正确的是（　　）
    A．两个物体只要接触就会产生弹力
    B．形状规则的物体，重心必与其几何中心重合
    C．同一地点，物体的重力与物体的质量成正比
    D．滑动摩擦力的方向总是和物体的运动方向相反

    分析 产生弹力的条件是接触且发生弹性形变，形状规则质量分布均匀的物体的重心必与其几何中心重合，物体受到的滑动摩擦力的方向一定和该物体的相对运动方向相反．

    解答 解：A、产生弹力的条件是接触且发生弹性形变，A错误；
    B、形状规则质量分布均匀的物体的重心必与其几何中心重合，B错误；
    C、根据G=mg，同一地点的重力加速度相同，则物体的重力与物体的质量成正比，C正确；
    D、某物体受到的滑动摩擦力的方向一定和该物体的相对运动方向相反，可能与运动方向相同，D错误；
    故选：C．

    点评 本题考查了弹力产生的条件，注意物体发生形变对与其接触的物体产生弹力作用．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中物理 来源： 题型：解答题

    9．如图所示，物体C与A的距离为3.5m，AC段的动摩擦因数为0.4．物体A、B用轻弹簧相连，物体B左侧与竖直墙相接触，AB段光滑．A、B的质量分别为mA=4.0kg、mB=6.0kg，物体C以速度v0=8m/s向左运动，与物体A相碰，碰后立即与A粘在一起不再分开，然后以v=2.0m/s的共同速度压缩弹簧，g=10m/s2，试求：
    ①物块C的质量mc；
    ②在B离开墙壁之前，弹簧的最大弹性势能．

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

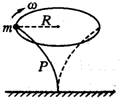    19．质量不计的轻质弹性杆P插在桌面上，杆端套有一个质量为m的小球，今使小球沿水平方向做半径为R的匀速圆周运动，角速度为ω，如图所示，则杆的上端受到的作用力大小为（　　）
    A．$\sqrt{{m^2}{g^2}+{m^2}{ω^4}{R^2}}$B．$\sqrt{{m^2}{g^2}-{m^2}{ω^4}{R^2}}$
    C．mω2RD．不能确定

    查看答案和解析>>

    科目：高中物理 来源： 题型：多选题

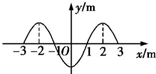    16．一列横波沿x轴传播，传播方向未知．t时刻与t+0.4s时刻波形相同，两时刻在x轴上-3m～3m的区间内的波形如图所示．下列说法中正确的是（　　）
    A．该波最大速度为10m/s
    B．质点振动的最小频率为2.5Hz
    C．在t+0.2s时刻，x=3m处的质点正在经过x轴
    D．若波沿x轴正方向传播，各质点刚开始振动时的方向向上
    E．该波的周期可能为0.025 s

    查看答案和解析>>

    科目：高中物理 来源： 题型：解答题

    3．如图1所示，两根足够长的平行金属导轨MN、PQ相距为L，导轨平面与水平面夹角为α，金属棒ab垂直于MN、PQ放置在导轨上，且始终与导轨接触良好，金属棒的质量为m．导轨处于匀强磁场中，磁场的方向垂直于导轨平面斜向上，磁感应强度大小为B．金属导轨的上端与开关S、定值电阻R1和电阻箱R2相连．不计一切摩擦，不计导轨、金属棒的电阻，重力加速度为g．现在闭合开关S，将金属棒由静止释放．

    （1）判断金属棒ab中电流的方向；
    （2）若电阻箱R2接入电路的阻值与R1相等，当金属棒下降高度为h时，速度为v，求此过程中定值电阻R1上产生的焦耳热Q；
    （3）当B=0.40T，L=0.50m，α=37°时，金属棒能达到的最大速度vm随电阻箱R2阻值的变化关系如图2所示，取g=10m/s2，sin37°=0.60，cos37°=0.80．求定值电阻R1的阻值和金属棒的质量m．

    查看答案和解析>>

    科目：高中物理 来源： 题型：多选题

    13．如果一个带电粒子以速率V进入一个匀强磁场，除磁场力外不受其它任何力的作用，则带电粒子在磁场中可能做（　　）
    A．匀加速直线运动B．匀速圆周运动C．匀速直线运动D．平抛运动

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    20．在物理学发展过程中，许多物理学家做出了杰出贡献，下列说法中错误的是（　　）
    A．奥斯特发现了电流的磁效应
    B．安培首先总结了电路中电流与电压和电阻的关系
    C．洛仑兹发现了磁场对运动电荷的作用规律
    D．法拉第对电磁感应现象进行了丰富的、开创性的研究

    查看答案和解析>>

    科目：高中物理 来源： 题型：选择题

    17．甲、乙两物体，在同一直线上运动，它们的加速度分别为a甲=4m/s2，a乙=-4m/s2，那么甲、乙两物体的运动情况是（　　）
    A．甲物体运动的加速度大于乙物体运动的加速度
    B．甲、乙两物体的运动方向一定相反
    C．甲做加速运动；乙做减速运动
    D．甲、乙两物体的加速度方向一定相反

    查看答案和解析>>

    科目：高中物理 来源： 题型：解答题

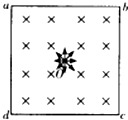    18．如图所示，在正方形区域abcd内充满方向垂直纸面向里的、磁感应强度为B的匀强磁场．在t=0时刻，一位于正方形区域中心O的粒子源在abcd平面内向各个方向发射出大量带正电的同种粒子，所有粒子的初速度大小均相同，粒子在磁场中做圆周运动的半径恰好等于正方形边长，不计重力和粒子之间的相互作用力．已知平行于ad方向发射的粒子在t=t0时刻刚好从磁场边界cd上的某点离开磁场，（已知sin$\frac{23π}{200}$=$\frac{\sqrt{2}}{4}$）求：
    （1）粒子的比荷$\frac{q}{m}$；
    （2）从粒子发射到粒子全部离开磁场所用的时间；
    （3）假设粒子源发射的粒子在各个方向均匀分布，在t=t0时刻仍在磁场中的粒子数与粒子发射的总粒子数之比．

    查看答案和解析>>

    同步练习册答案