
 ��ͼ��ʾ����Ǧȵ�б��������������Ϊd��ˮƽ���ߣ��ڢ���������ǿ�ų�����С��ΪB������ֱ��б�����£������߿�ABCD������Ϊm����Ϊ2d����ΪL������ΪR�������ͼʾλ�þ�ֹ�ͷţ�AB��λ�ڢ����ϱ߽磩��CD�ߵ�������ϱ߽�ʱ���߿�պ�������ֱ���˶�������һ��Ħ�����������ٶ�Ϊg����
��ͼ��ʾ����Ǧȵ�б��������������Ϊd��ˮƽ���ߣ��ڢ���������ǿ�ų�����С��ΪB������ֱ��б�����£������߿�ABCD������Ϊm����Ϊ2d����ΪL������ΪR�������ͼʾλ�þ�ֹ�ͷţ�AB��λ�ڢ����ϱ߽磩��CD�ߵ�������ϱ߽�ʱ���߿�պ�������ֱ���˶�������һ��Ħ�����������ٶ�Ϊg�������� ��1�����ݸ�Ӧ�����q=$\frac{��∅}{R}$�����ͨ����Ȧ�ĵ������
��2��CD�ߵ�������ϱ߽�ʱ���߿������˶�ʱ��������б�����µķ����밲����ƽ�⣬�Ƶ������������õ�V2����AB�뿪�ų�����CD�˶���JP������ϱ߽�Ĺ����У��߿����ȼ���ֱ���˶�����ţ�ٵڶ����ɿ���⣮
��3�����߿���ȫͨ�������ų��Ĺ������ɶ��ܶ����ɵ�
��� �⣺��1����AB��ͨ���ų�������ʱ���t���ڴ˹����У�$q=\overline I•��t$
$\overline I=\frac{\overline E}{R}$��$\overline E=\frac{����}{��t}$
��ã�$q=\frac{����}{R}=\frac{BLd}{R}$
��2����AB�߸��뿪�ų�����ʱ�߿������Ϊv1��CD�ߵ�������ϱ߽�ʱ�߿������Ϊv2��
�������֪��AB�߸��뿪�ų�������CD�ߵ�������ϱ߽�Ĺ����У��߿����ȼ���ֱ���˶���
CD�ߵ�������ϱ߽�ʱ���߿�պ�������ֱ���˶�����mgsin��=BIL��$I=\frac{{BL{v_2}}}{R}$
��ã�${v_2}=\frac{mgRsin��}{{{B^2}{L^2}}}$
AB���뿪�ų��������� mgsin��=ma���ã�a=gsin��
���ȱ���ֱ���˶��ã�$v_2^2-v_1^2=2a•3d$
��ã�${v_1}=\sqrt{\frac{{{m^2}{g^2}{R^2}{{sin}^2}��}}{{{B^4}{L^4}}}-6gdsin��}$
��3�����߿���ȫͨ�������ų��Ĺ������ɶ��ܶ����ɵã�
$mg•5dsin��+{W_{F��}}=\frac{1}{2}mv_2^2-0$
����ΪE=-WF��
���ԣ�$E=5mgdsin��-\frac{{{m^3}{g^2}{R^2}{{sin}^2}��}}{{2{B^4}{L^4}}}$
�𣺣�1��ABͨ���ų������Ĺ����У�ͨ����Ȧ�ĵ����$\frac{BLd}{R}$��
��2��AB���뿪�ų�����ʱ������Ϊ$\sqrt{\frac{{m}^{2}{g}^{2}{R}^{2}si{n}^{2}��}{{B}^{4}{L}^{4}}-6gdsin��}$��
��3���߿�ͨ�������ų��Ĺ����в����ĵ���$5mgdsin��-\frac{{m}^{3}{g}^{2}{R}^{2}si{n}^{2}��}{2{B}^{4}{L}^{4}}$��
���� �������Ĺؼ�������Ȧ���˶������ѡ����ʵĹ��ɽ�����⣬������ѵ����ͨ����Ȧ�ȼ���ֱ���˶��ھ��������ٶȣ�������ţ�ٵڶ�����������⣬���ܺ������������غ㶨�ɣ�


 ��ѧ����ͬ����ϰϵ�д�
��ѧ����ͬ����ϰϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
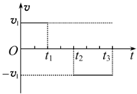 ��ͼ��ʾΪ������ֱ���˶���v-tͼ��������������˶�������s-tͼ���ʾ����������sΪ������Գ������λ�ƣ�����ͼ�е��ķ�ͼ������ȷ���ǣ�������
��ͼ��ʾΪ������ֱ���˶���v-tͼ��������������˶�������s-tͼ���ʾ����������sΪ������Գ������λ�ƣ�����ͼ�е��ķ�ͼ������ȷ���ǣ�������| A�� | 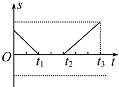 | B�� | 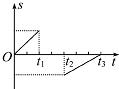 | C�� | 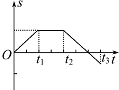 | D�� |  |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����������1.2g�ļ��ٶȼ������� | B�� | ����������1.2g�ļ��ٶȼ������� | ||
| C�� | ����������0.2g�ļ��ٶȼ����½� | D�� | ����������0.2g�ļ��ٶȼ����½� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
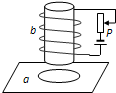 ��ͼ��ʾ��Բ���ε�����Ȧaƽ����ˮƽ�����ϣ���a�����Ϸ��̶�һ��ֱ���߹�b�����������غϣ����߹����Դ�ͻ������������ӳ���ͼ��ʾ�ĵ�·�����������������Ļ�ƬP���ϻ����������˵������ȷ���ǣ�������
��ͼ��ʾ��Բ���ε�����Ȧaƽ����ˮƽ�����ϣ���a�����Ϸ��̶�һ��ֱ���߹�b�����������غϣ����߹����Դ�ͻ������������ӳ���ͼ��ʾ�ĵ�·�����������������Ļ�ƬP���ϻ����������˵������ȷ���ǣ�������| A�� | ������Ȧa�Ĵ�ͨ����� | |
| B�� | ��Ȧa������������ | |
| C�� | ��Ȧa�н���������˳ʱ�뷽��ĸ�Ӧ���� | |
| D�� | ��Ȧa��ˮƽ�����ѹ��FN������ |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
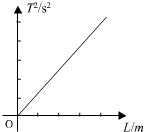 �ڡ��õ��ڲⶨ�������ٶȵ�ʵ���С�
�ڡ��õ��ڲⶨ�������ٶȵ�ʵ���С��鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | �¶ȵ͵���������һ��С | |
| B�� | �¶ȵ͵���������˶���ƽ������С | |
| C�� | �¶����ߣ��������˶���ƽ������һ�������������з��ӵ����ʶ����� | |
| D�� | ������������ʱ����������ܲ�һ������ | |
| E�� | ��Ȼ���н��е��漰������ĺ�۹��̶����з����� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ������
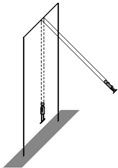 ����ǧ��һ����ϵ��˶�����ǧ��һ�����������ϵ�������̶���������ɣ���ij�˵�����Ϊm������ΪH��վ��ʱ������ŵ�$\frac{H}{2}$������ʱ������ŵ�$\frac{H}{4}$���������ҵ㵽̤�������Ϊ6H�������㹻�����Ҳ����쳤�����Ӻ�̤����������ƣ�������ʼ�������ӱ���ƽ�У��������ٶ�Ϊg��
����ǧ��һ����ϵ��˶�����ǧ��һ�����������ϵ�������̶���������ɣ���ij�˵�����Ϊm������ΪH��վ��ʱ������ŵ�$\frac{H}{2}$������ʱ������ŵ�$\frac{H}{4}$���������ҵ㵽̤�������Ϊ6H�������㹻�����Ҳ����쳤�����Ӻ�̤����������ƣ�������ʼ�������ӱ���ƽ�У��������ٶ�Ϊg���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
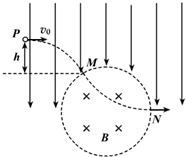 ij�ռ����һ��ֱ���µ���ǿ�糡��Բ���������ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱֽ�������ͼ��ʾ��һ����Ϊm��������Ϊ+q�����ӣ���P����ˮƽ�ٶ�v0����糡�У�Ȼ���M������ų�����N������ų�����֪���������Ӵ�M������ų�ʱ���ٶ�����ֱ�����30��ǣ���MN��Բ�ܳ���$\frac{1}{3}$�������������ƣ���
ij�ռ����һ��ֱ���µ���ǿ�糡��Բ���������ǿ�ų����Ÿ�Ӧǿ��ΪB������ֱֽ�������ͼ��ʾ��һ����Ϊm��������Ϊ+q�����ӣ���P����ˮƽ�ٶ�v0����糡�У�Ȼ���M������ų�����N������ų�����֪���������Ӵ�M������ų�ʱ���ٶ�����ֱ�����30��ǣ���MN��Բ�ܳ���$\frac{1}{3}$�������������ƣ����鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com