
 如图所示,光滑固定斜面倾角为θ=37°,斜面上有两个完全相同的正方形线框P、Q用细线连接,P通过平行于斜面的细线绕过斜面顶端的定滑轮与一重物相连接,开始重物固定,线框处于静止,斜面上水平虚线MN上方有垂直于斜面向下的匀强磁场,磁感应强度大小为B,线框的边长为L,线框间连线长及P线框最上边到MN的距离也为L,释放重物,使重物带动线框沿斜面向上运动,两个线框的质量均为m,每个线框的电阻均为R,重物的质量为2m,虚线上方的斜面足够长,重物离地面足够高,线框运动过程中,上边始终与MN平行,重力加速度为g,当线框P刚好要完全进入磁场的一瞬间,重物的加速度为零,求:
如图所示,光滑固定斜面倾角为θ=37°,斜面上有两个完全相同的正方形线框P、Q用细线连接,P通过平行于斜面的细线绕过斜面顶端的定滑轮与一重物相连接,开始重物固定,线框处于静止,斜面上水平虚线MN上方有垂直于斜面向下的匀强磁场,磁感应强度大小为B,线框的边长为L,线框间连线长及P线框最上边到MN的距离也为L,释放重物,使重物带动线框沿斜面向上运动,两个线框的质量均为m,每个线框的电阻均为R,重物的质量为2m,虚线上方的斜面足够长,重物离地面足够高,线框运动过程中,上边始终与MN平行,重力加速度为g,当线框P刚好要完全进入磁场的一瞬间,重物的加速度为零,求:分析 (1)根据系统机械能守恒求出线框P上边刚进入磁场时的速度,结合切割产生的感应电动势公式、安培力公式和欧姆定律求出安培力,分别隔分析,运用牛顿第二定律求出重物的加速度.
(2)根据法拉第电磁感应定律、闭合电路欧姆定律和电量的公式求出当线框P进入磁场的过程中,线框P中通过截面的电量;抓住线框P刚完全进入磁场时加速度为零,根据平衡求出速度,对系统,运用能量守恒求出产生的焦耳热.
(3)根据能量守恒求出线框Q刚进入磁场的速度,然后根据牛顿第二定律,运用微分思想求出线框Q刚好完全进入磁场时的速度.
解答 解:(1)线框P上边刚进入磁场时,根据机械能守恒有:
$2mgL-2mgLsinθ=\frac{1}{2}×4m{{v}_{1}}^{2}$,
对重物,根据牛顿第二定律有:
2mg-T=2ma,
对于两个线框,有:T-2mgsinθ-F安=2ma,
对于P线框回路:E=BLv1,$I=\frac{E}{R}$,
P线框所受的安培力F安=BIL,
联立解得a=$\frac{g}{5}-\frac{{B}^{2}{L}^{2}}{4mR}\sqrt{\frac{2}{5}gL}$.
(2)在线框P进入磁场的过程中,由q=$\overline{I}△t$,$\overline{I}=\frac{\overline{E}}{R}$,$\overline{E}=\frac{△Φ}{△t}$得:q=$\frac{△Φ}{R}=\frac{B{L}^{2}}{R}$,
当线框P刚要完全进入磁场的一瞬间,重物的加速度为零,则有:
$2mg×2L-2mg×2Lsinθ=\frac{1}{2}×4m{{v}_{2}}^{2}+$Q1,
$2mg=2mgsinθ+\frac{{B}^{2}{L}^{2}{v}_{2}}{R}$,
解得:Q1=$\frac{8}{5}mgL-\frac{32{m}^{3}{g}^{2}{R}^{2}}{25{B}^{4}{L}^{4}}$.
(3)设线框Q刚进入磁场时的速度为v3,刚好完全进入磁场时的速度为v4,则:
2mg×3L-2mg×3Lsinθ=$\frac{1}{2}×4m{{v}_{3}}^{2}+{Q}_{1}$,
线圈Q进入磁场的过程中,$2mg-2mgsinθ-\frac{{B}^{2}{L}^{2}v}{R}=4ma$,
$0.8mg-\frac{{B}^{2}{L}^{2}v}{R}=4m\frac{△v}{△t}$,
$0.8mg∑△t-\frac{{B}^{2}{L}^{2}}{R}∑v△t=4m∑△v$,即$0.8mgt-\frac{{B}^{2}{L}^{2}}{R}=4m({v}_{4}-{v}_{3})$,
联立解得v4=$0.2gt-\frac{{B}^{2}{L}^{2}}{4mR}+\sqrt{\frac{2}{5}gL+\frac{16{m}^{2}{g}^{2}{R}^{2}}{25{B}^{4}{L}^{4}}}$.
答:(1)线框P上边刚进入磁场时,重物的加速度为$\frac{g}{5}-\frac{{B}^{2}{L}^{2}}{4mR}\sqrt{\frac{2}{5}gL}$;
(2)当线框P进入磁场的过程中,线框P中通过截面的电量为$\frac{B{L}^{2}}{R}$,线框P中产生的焦耳热为$\frac{8}{5}mgL-\frac{32{m}^{3}{g}^{2}{R}^{2}}{25{B}^{4}{L}^{4}}$;
(3)如果线框Q进入磁场的过程所用的时间为t,则线框Q刚好完全进入磁场时的速度为$0.2gt-\frac{{B}^{2}{L}^{2}}{4mR}+\sqrt{\frac{2}{5}gL+\frac{16{m}^{2}{g}^{2}{R}^{2}}{25{B}^{4}{L}^{4}}}$.
点评 对于电磁感应与力学知识的综合,要正确分析线框的受力情况,利用安培力的表达式F=$\frac{{B}^{2}{L}^{2}v}{R}$求线框的速度是关键.本题物体较多,还要灵活选择研究对象.


 海淀课时新作业金榜卷系列答案
海淀课时新作业金榜卷系列答案 期末金牌卷系列答案
期末金牌卷系列答案 轻松课堂标准练系列答案
轻松课堂标准练系列答案科目:高中物理 来源: 题型:选择题
| A. | 欣赏姚明扣篮的动作时,姚明可视为质点 | |
| B. | 观看奥运冠军王军霞在万米长跑的名次时,王军霞可视为质点 | |
| C. | 欣赏“街舞”爱好者的优美舞姿时,“街舞”爱好者可视为质点 | |
| D. | 观看申雪、赵宏博双人滑的优美动作时,申雪、赵宏博可视为质点 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
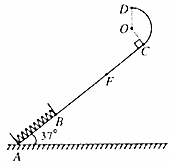 如图,一轻质弹簧原长为2R,其一端固定在倾角为37°的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然状态.直轨道与一半径为$\frac{24}{23}$R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高点到达F点,AF=4R,已知P与直轨道间的动摩擦因数μ=$\frac{1}{4}$,重力加速度大小为g.(取sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$)
如图,一轻质弹簧原长为2R,其一端固定在倾角为37°的固定直轨道AC的底端A处,另一端位于直轨道上B处,弹簧处于自然状态.直轨道与一半径为$\frac{24}{23}$R的光滑圆弧轨道相切于C点,AC=7R,A、B、C、D均在同一竖直面内.质量为m的小物块P自C点由静止开始下滑,最低到达E点(未画出),随后P沿轨道被弹回,最高点到达F点,AF=4R,已知P与直轨道间的动摩擦因数μ=$\frac{1}{4}$,重力加速度大小为g.(取sin37°=$\frac{3}{5}$,cos37°=$\frac{4}{5}$)查看答案和解析>>
科目:高中物理 来源: 题型:选择题
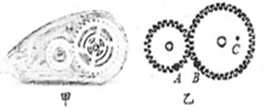
| A. | A和B的角速度相等 | B. | A的向心加速度不变 | ||
| C. | B和C的线速度大小相等 | D. | A的角速度大于C的角速度 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 如图所示,固定在水平面上的光滑平行金属导轨,间距为 L,右端接有阻值为 R 的电阻,空间存在在方向竖直、磁感应强度为 B 的匀强磁场.质量为 m、电阻为 r 的导体棒 ab 与固定弹簧相连,放在导轨上.初始时刻,弹簧恰处于自然长度.给导体棒水平向右的初速度 v0,导体棒开始 沿导轨往复运动,在此过程中,导体棒始终与导轨垂直并保持良好接触.已知导体棒的电阻 r 与定值电阻 R 的阻值 相等,不计导轨电阻,则下列说法中正确的是( )
如图所示,固定在水平面上的光滑平行金属导轨,间距为 L,右端接有阻值为 R 的电阻,空间存在在方向竖直、磁感应强度为 B 的匀强磁场.质量为 m、电阻为 r 的导体棒 ab 与固定弹簧相连,放在导轨上.初始时刻,弹簧恰处于自然长度.给导体棒水平向右的初速度 v0,导体棒开始 沿导轨往复运动,在此过程中,导体棒始终与导轨垂直并保持良好接触.已知导体棒的电阻 r 与定值电阻 R 的阻值 相等,不计导轨电阻,则下列说法中正确的是( )| A. | 金属棒最终会停在初始位置的右端 | |
| B. | 导体棒开始运动的初始时刻导体棒两端的电压U=BLv0 | |
| C. | 导体棒开始运动后速度第一次为零时,系统的弹性势能Ep=$\frac{1}{2}$mv02 | |
| D. | 在金属棒整个运动过程中,电阻R上产生的焦耳热Q=$\frac{1}{4}$mv02 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
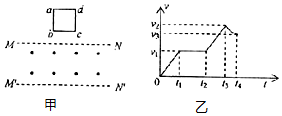 如图甲所示,正方形金属线框abcd位于竖直平面内,其质量为m,电阻为R,在线框的下方有一匀强磁场,MN和M′N′是磁场的水平边界,并与bc边平行,磁场方向垂直于纸面向外,现使金属线框从MN上方某一高度处由静止开始下落.图乙是金属线框由开始下落到完全穿过匀强磁场区域瞬间的v-t图象,图象中字母均为已知量.重力加速度为g,不计空气阻力,下列说法正确的是( )
如图甲所示,正方形金属线框abcd位于竖直平面内,其质量为m,电阻为R,在线框的下方有一匀强磁场,MN和M′N′是磁场的水平边界,并与bc边平行,磁场方向垂直于纸面向外,现使金属线框从MN上方某一高度处由静止开始下落.图乙是金属线框由开始下落到完全穿过匀强磁场区域瞬间的v-t图象,图象中字母均为已知量.重力加速度为g,不计空气阻力,下列说法正确的是( )| A. | 金属线框的边长为v1t2 | |
| B. | 磁场的磁感应强度为$\frac{1}{{v}_{1}({t}_{2}-{t}_{1})}$$\sqrt{\frac{mgR}{{v}_{1}}}$ | |
| C. | 金属线框完全进入磁场后感应电流方向沿adcba方向 | |
| D. | 金属线框在0~t4的时间内所产生的热量为2mgv1(t2-t1)+$\frac{1}{2}$m(v32-v22) |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
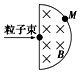 如图所示为一半圆形的匀强磁场B,当一束粒子对着圆心射入该磁场,发现所有粒子都从M点射出,下列说法正确的是( )
如图所示为一半圆形的匀强磁场B,当一束粒子对着圆心射入该磁场,发现所有粒子都从M点射出,下列说法正确的是( )| A. | 这束粒子全部带负电荷 | |
| B. | 这束粒子全部带正电荷 | |
| C. | 这束粒子全部不带电 | |
| D. | 这束粒子中有的带正电荷,有的带负电荷 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
 “天宫一号”目标飞行器未变轨前绕地球运行轨道可视为圆形轨道,如图所示,当“天宫一号”按逆时针方向运动到轨道A点时,它的( )
“天宫一号”目标飞行器未变轨前绕地球运行轨道可视为圆形轨道,如图所示,当“天宫一号”按逆时针方向运动到轨道A点时,它的( )| A. | 线速度方向是v1的方向 | B. | 线速度方向是v2的方向 | ||
| C. | 运行速率大于7.9 km/s | D. | 运行速率大于11.2km/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
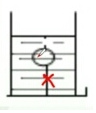 一个盛水的杯子放在水平面上,用一根细线拴住一个木球使其与杯子保持静止如图,若剪断绳子,球剪断绳子的瞬间地面对杯子的支持力( )
一个盛水的杯子放在水平面上,用一根细线拴住一个木球使其与杯子保持静止如图,若剪断绳子,球剪断绳子的瞬间地面对杯子的支持力( )| A. | 变大 | B. | 变小 | C. | 不变 | D. | 无法判定 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com