
 ��ͼ��ʾ���ס�������С������һ��������ˮƽ����������Ϸ�������ı�����������Ϊ30kg���Һ����ı���������ҲΪ30kg����Ϸʱ��������һ������Ϊ15kg�����Ӻ���һ����2m/s���ٶȻ��У�����ͬ����С���ٶ�ӭ�滬����Ϊ�˱�����ײ����ͻȻ�������ر����Ƹ��ң����ӻ����Ҵ�ʱ��Ѹ�ٰ���ץס�����Ʊ����Ħ����
��ͼ��ʾ���ס�������С������һ��������ˮƽ����������Ϸ�������ı�����������Ϊ30kg���Һ����ı���������ҲΪ30kg����Ϸʱ��������һ������Ϊ15kg�����Ӻ���һ����2m/s���ٶȻ��У�����ͬ����С���ٶ�ӭ�滬����Ϊ�˱�����ײ����ͻȻ�������ر����Ƹ��ң����ӻ����Ҵ�ʱ��Ѹ�ٰ���ץס�����Ʊ����Ħ�������� ��1��ǡ�ò���ײ���ٽ�������ҽӵ����Ӻ��ҵ��ٶ���ȣ��Լ��ҡ�����������ɵ�ϵͳ�о�����϶����غ�������߹�ͬ���ٶȣ��ٶԼ�������ɵ�ϵͳ���ö����غ㣬������Ƴ����ӵ��ٶ���С�ٶȣ�
��2���������ӵij�ĩ�ٶȣ���϶�����������������ӹ����ж����ӵij�����С��
��� �⣺��1��ǡ�ò���ײ��ӦΪ�ҽӵ����Ӻ�ס����ٶ���ȣ��涨����Ϊ�����Ը�ϵͳ�ɶ����غ㶨�ɵã�
��M+m��v0-Mv0=��2M+m��v��
�������ݽ�ã�v=0.4m/s��
�������ӹ��̣��涨����Ϊ�������ɶ����غ㶨�ɵã���M+m��v0=Mv+mvm��
�������ݽ�ã�vm=5.2m/s��
��2�������ӹ��̣��������ɶ��������ã�I=m��vm-v0����
�������ݽ�ã�I=48N•s��
�𣺣�1��������Ҫ��5.2m/s���ٶȽ������Ƴ������ܱ���������ײ��
��2���������ӹ����ж����ӵij���Ϊ48N•s��
���� ���⿼���˶����غ�Ͷ��������Ļ������ã��ؼ�������ѡ��ϵͳ��ץס�ٽ��������϶����غ㶨�ɽ�����⣬�ѶȲ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ���������� ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
 ����Ϊm2������ΪL��С����ֹ�ڹ⻬ˮƽ���ϣ�С�������վ��������Ϊm1���ˣ�С�����Ҷ�վ��������Ϊm3���ˣ���m1��m3�����˴Ӿ�ֹ��ʼ�����˶�������λ�ã���˹�����С����λ�Ʒ���ʹ�СΪ��������
����Ϊm2������ΪL��С����ֹ�ڹ⻬ˮƽ���ϣ�С�������վ��������Ϊm1���ˣ�С�����Ҷ�վ��������Ϊm3���ˣ���m1��m3�����˴Ӿ�ֹ��ʼ�����˶�������λ�ã���˹�����С����λ�Ʒ���ʹ�СΪ��������| A�� | С�����ƣ�λ�ƴ�СΪ$\frac{{m}_{1}+{m}_{3}}{{m}_{1}+{m}_{2}+{m}_{3}}$L | |
| B�� | С�����ƣ�λ�ƴ�СΪ$\frac{{m}_{1}-m3}{{m}_{1}+{m}_{2}+{m}_{3}}$L | |
| C�� | С�����ƣ�λ�ƴ�СΪ$\frac{��{m}_{1}+{m}_{3}��-{m}_{2}}{{m}_{1}+{m}_{2}+{m}_{3}}$L | |
| D�� | С�����ƣ�λ�ƴ�СΪ$\frac{{m}_{2}-��{m}_{1}+{m}_{3}��}{{m}_{1}+{m}_{2}+{m}_{3}}$L |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
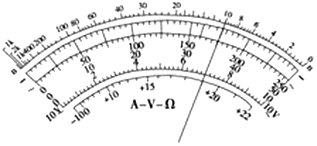
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ʵ����
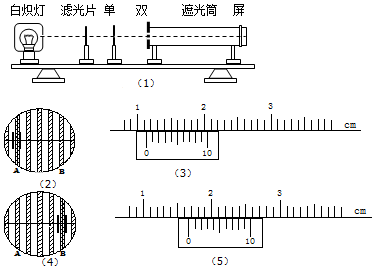 ����ͼ��װ���о�˫���������
����ͼ��װ���о�˫����������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
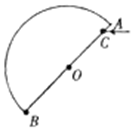 ��ˮƽ�����Ϸ�����һ�뾶ΪR�İ�Բ�β���ש��ֱ��AB��ˮƽ����ļн�Ϊ45�㣬һ�����ߴ�C��ˮƽ���벣��ש�У�OC=$\frac{\sqrt{6}}{3}$R����֪���벣��ש�Ĺ��ߵ�һ�ε��ﲣ��ש��Եʱ��ǡ�ò��Ӳ���ש�������
��ˮƽ�����Ϸ�����һ�뾶ΪR�İ�Բ�β���ש��ֱ��AB��ˮƽ����ļн�Ϊ45�㣬һ�����ߴ�C��ˮƽ���벣��ש�У�OC=$\frac{\sqrt{6}}{3}$R����֪���벣��ש�Ĺ��ߵ�һ�ε��ﲣ��ש��Եʱ��ǡ�ò��Ӳ���ש��������鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�������
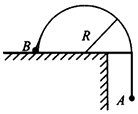 ��ͼ��ʾ��һ�������Ϊ��Բ���뾶ΪR�Ĺ⻬���棬һ�������쳤��ϸ�����˷ֱ�ϵ������A��B����mA=2mB����ͼʾλ�ôӾ�ֹ��ʼ�ͷ�A���壬������B�ﵽԲ������ʱ��
��ͼ��ʾ��һ�������Ϊ��Բ���뾶ΪR�Ĺ⻬���棬һ�������쳤��ϸ�����˷ֱ�ϵ������A��B����mA=2mB����ͼʾλ�ôӾ�ֹ��ʼ�ͷ�A���壬������B�ﵽԲ������ʱ���鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ�ѡ����
| A�� | ����A�ļ��ٶȴ� | B�� | ����A���ٶȱ仯�� | ||
| C�� | ����B�ļ��ٶȴ� | D�� | ����B���ٶȱ仯�� |
�鿴�𰸺ͽ���>>
��Ŀ���������� ��Դ�� ���ͣ���ѡ��
| A�� | ���������Ĺ�Ϊ$\frac{ma-��gx}{1+��tan��}$ | |
| B�� | ���������Ĺ�Ϊ$\frac{ma+��mg}{cos��-��sin��}$ | |
| C�� | ľ��˷�Ħ�������Ĺ�Ϊ�̣�mg+macos��x | |
| D�� | ľ��˷�Ħ�������Ĺ�Ϊ$\frac{��ma-gcot��}{cot��-��}x$ |
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com