
从地球表面向火星发射火星探测器。设地球和火星都在同一平面上绕太阳做匀速圆周运动。火星轨道半径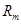 为地球轨道半径
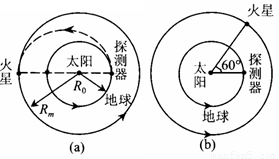
为地球轨道半径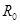 的1.5倍。简单而又比较节省能量的发射过程可分为两步进行:第一步,在地球表面用火箭对探测器进行加速,使之获得足够的动能,成为一个绕地球运行的人造卫星;第二步,在适当时刻点燃与探测器连在一起的火箭发动机。在短时间内对探测器沿原方向加速,使其速度数值增加到适当值,使探测器沿半个椭圆轨道(该椭圆长轴两端分别与地球公转轨道及火星公转轨道相切)射到火星上。如图(a)所示。已知地球半径
的1.5倍。简单而又比较节省能量的发射过程可分为两步进行:第一步,在地球表面用火箭对探测器进行加速,使之获得足够的动能,成为一个绕地球运行的人造卫星;第二步,在适当时刻点燃与探测器连在一起的火箭发动机。在短时间内对探测器沿原方向加速,使其速度数值增加到适当值,使探测器沿半个椭圆轨道(该椭圆长轴两端分别与地球公转轨道及火星公转轨道相切)射到火星上。如图(a)所示。已知地球半径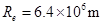 ,重力加速度g=10m/s2。
,重力加速度g=10m/s2。
(1)为使探测器成为绕地球运行的人造卫星,探测器在地面附近至少要获得多大的速度(不考虑地球自转)。
(2)求火星探测器的飞行时间为多少天(已知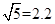 ,1年为365天)。
,1年为365天)。
(3)当探测器绕地球运行稳定后,在某年 3月 1 日零时测得探测器与火星之间的角度为 60°,如图(b)所示。求应在何年何月何日点燃探测器上的火箭发动机方能使探测器恰好落在火星表面(时间计算仅需精确到天,已知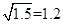 ,1年为365天)。
,1年为365天)。
(1)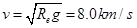 (2)
(2)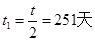 (3)即同年的 4月11日
(3)即同年的 4月11日
【解析】(1)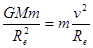
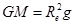
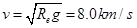
(2)探测器和地球都围绕太阳运动,设探测器的周期为t,地球周期为T0。依据开普勒第三定律有:
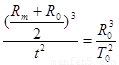
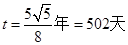 探测器的飞行时间
探测器的飞行时间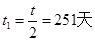
(3))为使探测器沿椭圆轨道到达与火星轨道的相切点时,火星恰好运行到这一点,必须选择适当时机点燃火箭发动机。
地球公转的运动周期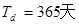
地球公转的角速度 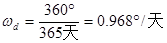
火星公转周期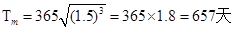
火星公转角速度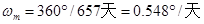
探测器从点燃火箭发动机至到达火星所需时间为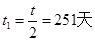
探测器运行至火星的251天内,火星运行的角度为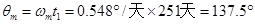
为了使探测器到达火星轨道时,正好射到火星上,那么探测器在椭圆轨道近日点点燃火箭发动机时,火星应在其远日点的切点之前137.5°处,即探测器点燃发动机时,与火星的角度应为180°-137.5°=42.5°
但是,已知某年3月1日零时探测器与火星的角距离为 60°(火星在前,探测器在后),为使其角度成为 42.5°,必须等待一段时间,设为t天,使二者达到角距离42.5°的合适位置。t 满足
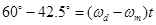
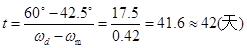
因此点燃火箭发动机的时刻应为当年的 3月1日之后42天,即同年的 4月11日
本题考查圆周运动的规律和万有引力定律的应用,可以根据开普勒第三定律求解第二问,借助几何关系求解第三问


 新课标快乐提优暑假作业陕西旅游出版社系列答案
新课标快乐提优暑假作业陕西旅游出版社系列答案 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案科目:高中物理 来源: 题型:
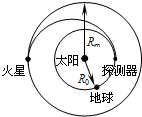 从地球表面向火星发射火星探测器,设地球和火星都在同一平面上绕太阳做圆周运动,地球轨道半径为R0,火星轨道半径Rm为1.5R0,发射过程可分为两步进行:第一步,在地球表面用火箭对探测器进行加速,使之获得足够的动能,从而脱离地球引力作用成为一个沿地球轨道绕太阳运行的人造行星;第二步是在适当时刻点燃与探测器连在一起的火箭发动机,在短时间内对探测器沿原方向加速使其速度数值增加到适当值,从而使得探测器沿着一个与地球轨道及火星轨道分别在长轴两端相切的半个椭圆,正好射到火星上,如图所示.已知地球绕太阳公转周期为一年,万有引力常量为G,则( )
从地球表面向火星发射火星探测器,设地球和火星都在同一平面上绕太阳做圆周运动,地球轨道半径为R0,火星轨道半径Rm为1.5R0,发射过程可分为两步进行:第一步,在地球表面用火箭对探测器进行加速,使之获得足够的动能,从而脱离地球引力作用成为一个沿地球轨道绕太阳运行的人造行星;第二步是在适当时刻点燃与探测器连在一起的火箭发动机,在短时间内对探测器沿原方向加速使其速度数值增加到适当值,从而使得探测器沿着一个与地球轨道及火星轨道分别在长轴两端相切的半个椭圆,正好射到火星上,如图所示.已知地球绕太阳公转周期为一年,万有引力常量为G,则( )