
 如图所示,两根等高光滑的$\frac{1}{4}$圆弧轨道,半径为r、间距为L,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、质量为m、电阻不计的金属棒从轨道的顶端ab处由静止开始下滑,到达轨道底端cd时受到轨道的支持力为2mg.整个过程中金属棒与导轨电接触良好,求:
如图所示,两根等高光滑的$\frac{1}{4}$圆弧轨道,半径为r、间距为L,轨道电阻不计.在轨道顶端连有一阻值为R的电阻,整个装置处在一竖直向上的匀强磁场中,磁感应强度为B.现有一根长度稍大于L、质量为m、电阻不计的金属棒从轨道的顶端ab处由静止开始下滑,到达轨道底端cd时受到轨道的支持力为2mg.整个过程中金属棒与导轨电接触良好,求:分析 (1)金属棒在cd端时由重力和轨道的支持力的合力提供向心力,根据牛顿第二定律求出棒到达最低点时的速度.由E=BLv求出感应电动势,再由欧姆定律求通过R的电流.
(2)根据能量守恒定律求回路中产生的焦耳热.根据法拉第电磁感应定律、欧姆定律和电量公式推导出电量表达式q=$\frac{△Φ}{R}$,来求通过R的电荷量.
(3)①棒沿轨道做匀速圆周运动,求出金属棒在运动过程中水平方向的分速度vx,再由E=BLvx求瞬时感应电动势.
②金属棒切割磁感线产生余弦交变电,求感应电动势的有效值,再由功能关系求拉力做的功.
解答 解:(1)棒在最低点,根据牛顿第二定律得
N-mg=m$\frac{{v}^{2}}{r}$
由题得 N=2mg
可得 v=$\sqrt{gr}$
棒经过最低点时产生的感应电动势为 E=BLv=BL$\sqrt{gr}$
通过电阻R的电流 I=$\frac{E}{R}$=$\frac{BL}{R}$$\sqrt{gr}$
(2)整个过程中系统能量守恒得:
回路中产生的焦耳热 Q=mgr-$\frac{1}{2}m{v}^{2}$=$\frac{1}{2}$mgr
根据法拉第电磁感应定律得:
$\overline{E}$=$\frac{△Φ}{△t}$
感应电流的平均值 $\overline{I}$=$\frac{\overline{E}}{R}$
通过R的电荷量 q=$\overline{I}$△t
联立得 q=$\frac{△Φ}{R}$
又△Φ=BLr
所以可得 q=$\frac{BLr}{R}$
(3)①金属棒在运动过程中水平方向的分速度 vx=v0cosωt
又 v0=ωr
金属棒切割磁感线产生的余弦交变电:e=BLvx=BLv0cos$\frac{{v}_{0}t}{r}$
②四分之一周期内,电流的有效值:I=$\frac{BL{v}_{0}}{\sqrt{2}R}$
由能量守恒得:拉力做的功 W=mgr+Q
由焦耳定律得 Q=I2R$\frac{T}{4}$
T=$\frac{2πr}{{v}_{0}}$
解得:W=mgr+$\frac{πr{B}^{2}{L}^{2}{v}_{0}}{4R}$
答:
(1)棒到达最低点时的速度大小是$\sqrt{gr}$,通过电阻R的电流是$\frac{BL}{R}$$\sqrt{gr}$.
(2)棒从ab下滑到cd过程中回路中产生的焦耳热是$\frac{1}{2}$mgr,通过R的电荷量是$\frac{BLr}{R}$.
(3)①杆在运动过程中产生的瞬时感应电动势随时间t的变化关系是e=BLv0cos$\frac{{v}_{0}t}{r}$.
②在杆到达ab的过程中拉力做的功为mgr+$\frac{πr{B}^{2}{L}^{2}{v}_{0}}{4R}$.
点评 本题是电磁感应与力学知识的综合,要正确分析能量是如何转化的,熟练推导出感应电荷量经验公式q=$\frac{△Φ}{R}$,要注意R是回路中总的电阻.


科目:高中物理 来源: 题型:实验题
| 1 | 2 | 3 | 4 | 5 | |
| L(m) | 0.600 | 0.800 | 1.000 | 1.200 | 1.400 |
| t(ms) | 8.22 | 7.17 | 6.44 | 5.85 | 5.43 |
| $\frac{1}{{t}^{2}}$(104s-2) | 1.48 | 1.95 | 2.41 | 2.92 | 3.39 |

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 路程和位移的大小均为 3.5 πR | B. | 路程和位移的大小均为 2R | ||
| C. | 路程为 3.5 πR,位移的大小为 $\sqrt{2}$R | D. | 路程为 0.5 πR,位移的大小为 2R |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 用长为L的金属导线将一小球A悬挂于O点,小球A在水平面内做匀速圆周运动,整个装置处于竖直向下的匀强磁场中,磁感应强度大小为B,已知小球A做圆周运动的角速度为ω,金属导线与竖直方向的夹角为30°,求:金属导线中产生的感应电动势E.
用长为L的金属导线将一小球A悬挂于O点,小球A在水平面内做匀速圆周运动,整个装置处于竖直向下的匀强磁场中,磁感应强度大小为B,已知小球A做圆周运动的角速度为ω,金属导线与竖直方向的夹角为30°,求:金属导线中产生的感应电动势E.查看答案和解析>>
科目:高中物理 来源: 题型:解答题
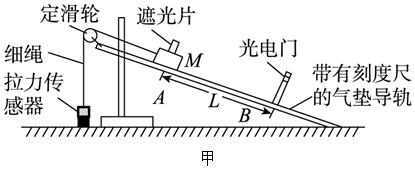
 如图所示,在一个光滑金属框架上垂直放置一根长l=0.4m的金属棒ab,其电阻r=0.1Ω.框架左端的电阻R=0.4Ω.垂直框面的匀强磁场的磁感强度B=0.1T.当用外力使棒ab以速度v=5m/s匀速向右移时,求:
如图所示,在一个光滑金属框架上垂直放置一根长l=0.4m的金属棒ab,其电阻r=0.1Ω.框架左端的电阻R=0.4Ω.垂直框面的匀强磁场的磁感强度B=0.1T.当用外力使棒ab以速度v=5m/s匀速向右移时,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
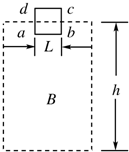 如图,正方形导线框abcd的边长为L=10cm,线框平面位于竖直平面内,上下两边处于水平状态.当它从某高处落下时通过一匀强磁场,磁场方向垂直于线框平面,线框的ab边刚进入磁场时,由于安培力的作用使得线框恰能匀速运动.已知磁场的宽度h=4L,线框刚进入磁场时的速度v0=2.5m/s.那么若以向下为力的正方向,则线框通过磁场区域过程中所受安培力的图象可能是以下四图中的( )
如图,正方形导线框abcd的边长为L=10cm,线框平面位于竖直平面内,上下两边处于水平状态.当它从某高处落下时通过一匀强磁场,磁场方向垂直于线框平面,线框的ab边刚进入磁场时,由于安培力的作用使得线框恰能匀速运动.已知磁场的宽度h=4L,线框刚进入磁场时的速度v0=2.5m/s.那么若以向下为力的正方向,则线框通过磁场区域过程中所受安培力的图象可能是以下四图中的( )| A. | 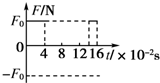 | B. |  | ||
| C. |  | D. |  |
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
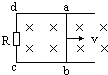
 将两根粗糙的平行放置的直导轨MN、PQ固定在水平面上,左端与两根弯曲的光滑导轨平滑连接,在两水平导轨间存在两个磁场区,其中左侧的磁场方向竖直向上,磁感应强度大小为B,磁场的左边界位于水平导轨和弯曲导轨连接处;右侧的磁场方向竖直向下,磁感应强度大小为2B,如图所示,今将一导体棒b垂直导轨放置在右侧磁场的右边界处,导体棒a从弯曲导轨上距离水平面h高处由静止释放.已知两棒的质量均为m,二者在导轨间部分的电阻均为R,两导轨之间的距离为L,两导体棒与水平轨道间的动靡擦因数均为0.2,假设导体棒与导轨间的最大静摩擦力等于滑动摩擦力,整个运动过程中导体棒与导轨的接触始终良好,导轨的电阻不计,重力加速度为g.
将两根粗糙的平行放置的直导轨MN、PQ固定在水平面上,左端与两根弯曲的光滑导轨平滑连接,在两水平导轨间存在两个磁场区,其中左侧的磁场方向竖直向上,磁感应强度大小为B,磁场的左边界位于水平导轨和弯曲导轨连接处;右侧的磁场方向竖直向下,磁感应强度大小为2B,如图所示,今将一导体棒b垂直导轨放置在右侧磁场的右边界处,导体棒a从弯曲导轨上距离水平面h高处由静止释放.已知两棒的质量均为m,二者在导轨间部分的电阻均为R,两导轨之间的距离为L,两导体棒与水平轨道间的动靡擦因数均为0.2,假设导体棒与导轨间的最大静摩擦力等于滑动摩擦力,整个运动过程中导体棒与导轨的接触始终良好,导轨的电阻不计,重力加速度为g.查看答案和解析>>
科目:高中物理 来源: 题型:多选题
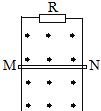 一回路竖直放置在匀强磁场中,磁场方向与回路垂直,导线MN可自由地沿足够长的光滑导轨运动,回路电阻除R外均忽略不计,如图所示.当MN无初速释放后,则下列说法正确的是( )
一回路竖直放置在匀强磁场中,磁场方向与回路垂直,导线MN可自由地沿足够长的光滑导轨运动,回路电阻除R外均忽略不计,如图所示.当MN无初速释放后,则下列说法正确的是( )| A. | MN受到磁场阻力,以小于g的加速度向下做匀加速直线运动 | |
| B. | MN加速下落,最后趋向于一个恒定的收尾速度 | |
| C. | 回路中的电流越来越大,最后趋于一个恒定的极限值 | |
| D. | MN受到的磁场力越来越大,最后和导线MN的重力相平衡 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com