解答:解:(1)正离子在两金属板间受到电场力而作匀加速直线运动,离开电场后做匀速直线运动,进入磁场后受到洛伦兹力而做匀速圆周运动,离开磁场后,离子又做匀速直线运动,直到打在荧光屏上.
(2)设离子由电场射出后进入磁场时的速度为v.因离子是沿圆心O的方向射入磁场,由对称性可知,离子射出磁场时的速度方向的反向延长线也必过圆心O.离开磁场后,离子垂直打在荧光屏上(图中的O′点),则离子在磁场中速度方向偏转了90°,由几何知识可知,离子在磁场中做圆周运动的半径
r′=R=10
cm①
设离子的电荷量为q、质量为m,进入磁场时的速度为v有
由qvB=m
得
r′= ②
设两金属板间的电压为U,离子在电场中加速,由动能定理有:
qU=mv2③
而
=2×105C/kg ④
由②③两式可得U=
⑤
代入有关数值可得U=30V,也就是电压表示数为30V.
(3)因两金属板间的电压越小,离子经电场后获得的速度也越小,离子在磁场中作圆周运动的半径越小,射出电场时的偏转角越大,也就越可能射向荧光屏的左侧.
由闭合电路欧姆定律有,I=
=1A.
当滑动片P处于最右端时,两金属板间电压最大,为U
max=I(R
1+R
2)=90V
当滑动片P处于最左端时,两金属板间电压最小,为U
min=IR
1=10V
两板间电压为U
min=10V时,离子射在荧光屏上的位置为所求范围的最左端点,由②③可解得离子射出电场后的速度大小为v
1=2×10
3m/s,离子在磁场中做圆运动的半径为r
1=0.1m.
此时粒子进入磁场后的径迹如图答2所示,O
1为径迹圆的圆心,A点为离子能射到荧光屏的最左端点.由几何知识可得:
tan=
=
,所以α=60°
所以AO′=Htan(90°-α)=2×
10×cm=20cm
而两板间电压为U
max=90V时,离子射在荧光屏上的位置为所求范围的最右端点,此时粒子进入磁场后的径迹如图答3所示,
同理由②③可解得离子射出电场后的速度大小为v
1=6×10
3m/s,离子在磁场中做圆运动的半径为r
1=0.3m,或直接由⑤式求得r
2=0.3m
由几何知识可得tan
==即β=120°
所以O′B=Htan(β-90°)=2×10
×cm=20cm
离子到达荧光屏上的范围为以O′为中点的左右两侧20cm.
答:(1)正离子自S
1到荧光屏D的运动情况是正离子在两金属板间作匀加速直线运动,离开电场后做匀速直线运动,进入磁场后做匀速圆周运动,离开磁场后,离子又做匀速直线运动,直到打在荧光屏上.
(2)如果正离子垂直打在荧光屏上,电压表的示数30V.
(3)调节滑动变阻器滑片P的位置,正离子到达荧光屏的最大范围是以O′为中点的左右两侧20cm.

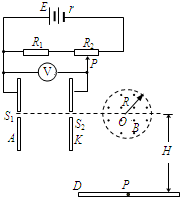 如图所示,在以O为圆心,半径为R=10
如图所示,在以O为圆心,半径为R=10

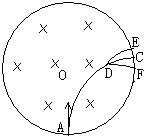 (2004?惠州一模)如图所示,在一个半径为R的圆形区域内存在着匀强磁场,磁场方向垂直于圆面向里,一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内,粒子将做圆周运动到达磁场边界的C点,但在粒子经过D点时,恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子,关于这个新粒子的运动情况,以下判断正确的是( )
(2004?惠州一模)如图所示,在一个半径为R的圆形区域内存在着匀强磁场,磁场方向垂直于圆面向里,一个带电粒子从磁场边界的A点以指向圆心O的方向进入磁场区域内,粒子将做圆周运动到达磁场边界的C点,但在粒子经过D点时,恰好与一个原来静止在该点的不带电的粒子碰撞后结合在一起形成新粒子,关于这个新粒子的运动情况,以下判断正确的是( ) 如图所示,在圆心O处固定一正点电荷,现从P点以相同的速率发射两个检验电荷a、b,分别沿PM、PN运动到M、N两点,M、N都在以O为圆心的圆上.若检验电荷a、b的质量、电荷量均相等,则下列判断正确的是( )
如图所示,在圆心O处固定一正点电荷,现从P点以相同的速率发射两个检验电荷a、b,分别沿PM、PN运动到M、N两点,M、N都在以O为圆心的圆上.若检验电荷a、b的质量、电荷量均相等,则下列判断正确的是( ) 如图所示,在圆心O处固定一正点电荷,两个质量和电量均相同的检验电荷a、b从P点以相同的速率,分别沿PN、PM运动到N、M(均在以O为圆心的圆上),下列说法正确的是( )
如图所示,在圆心O处固定一正点电荷,两个质量和电量均相同的检验电荷a、b从P点以相同的速率,分别沿PN、PM运动到N、M(均在以O为圆心的圆上),下列说法正确的是( )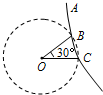 如图所示,在点O置于一个正点电荷,在过点O的竖直平面内的点A处,自由释放一个带正电的小球,小球的质量为m,带电量为q,小球落下的轨迹如图中实线所示,它与以O为圆心,R为半径的圆相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC高度为h,若小球过B点时的速度为v,则( )
如图所示,在点O置于一个正点电荷,在过点O的竖直平面内的点A处,自由释放一个带正电的小球,小球的质量为m,带电量为q,小球落下的轨迹如图中实线所示,它与以O为圆心,R为半径的圆相交于B、C两点,点O、C在同一水平线上,∠BOC=30°,点A距OC高度为h,若小球过B点时的速度为v,则( )![]() ,竖直平行放置的金属板连接在如图所示的电路中,电源电动势E=91V,内阻r=1Ω,定值电阻
,竖直平行放置的金属板连接在如图所示的电路中,电源电动势E=91V,内阻r=1Ω,定值电阻![]() ,滑动变阻器
,滑动变阻器![]() 的最大阻值为70Ω;两金属板上的小孔
的最大阻值为70Ω;两金属板上的小孔![]() 、
、![]() 跟O点在垂直于极板的同一直线上,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D之间的距离
跟O点在垂直于极板的同一直线上,另有一水平放置的足够长的荧光屏D,O点跟荧光屏D之间的距离![]() ,现有比荷
,现有比荷![]() 的正正离子由小孔
的正正离子由小孔![]() 进入电场加速后,从小孔
进入电场加速后,从小孔![]() 穿出,通过磁场后打在荧光屏D上,不计离子的重力和离子在小孔
穿出,通过磁场后打在荧光屏D上,不计离子的重力和离子在小孔![]() 处的初速度,问:
处的初速度,问:![]() 点的距离。
点的距离。