
 如图所示,足够长的金属导轨MN、PQ平行放置,间距为L=0.5m,与水平面成θ=30°角,导轨与定值电阻R1和R2相连,且R1=R2=2Ω,R1支路串联开关S,原来S闭合.匀强磁场垂直导轨平面向上,有一质量为m=1.6kg、长度为L=0.5m、电阻为r=2Ω的导体棒ab与导轨垂直放置,它与导轨的接触粗糙且始终接触良好,现让导体棒ab从静止开始释放,沿导轨下滑,当导体棒运动达到稳定状态时速率为v=2m/s,此时整个电路消耗的电功率为重力功率的$\frac{3}{4}$.重力加速度g取10m/s2,导轨电阻不计,求:
如图所示,足够长的金属导轨MN、PQ平行放置,间距为L=0.5m,与水平面成θ=30°角,导轨与定值电阻R1和R2相连,且R1=R2=2Ω,R1支路串联开关S,原来S闭合.匀强磁场垂直导轨平面向上,有一质量为m=1.6kg、长度为L=0.5m、电阻为r=2Ω的导体棒ab与导轨垂直放置,它与导轨的接触粗糙且始终接触良好,现让导体棒ab从静止开始释放,沿导轨下滑,当导体棒运动达到稳定状态时速率为v=2m/s,此时整个电路消耗的电功率为重力功率的$\frac{3}{4}$.重力加速度g取10m/s2,导轨电阻不计,求:分析 (1)当导体棒匀速运动时达到稳定状态,此时速率为V,重力功率为mgVsinθ.由E=BLV、I=$\frac{E}{{R}_{总}}$、
P电=I2R总,得到回路的总电功率P电,根据电功率为重力功率的$\frac{3}{4}$,列式求磁感应强度B.并求出通过ab棒的电流I;
(2)根据重力功率等于电功率与克服摩擦力做功功率之和,列式求出摩擦力大小,由能量守恒求回路中产生的电热;
(3)S断开后,由法拉第电磁感应定律、欧姆定律和电量公式q=It,得到电量q与距离的关系,即可求出距离;
(4)当断开后,根据安培力与速度的关系,结合牛顿第二定律与运动学公式,即可求解.
解答 解:(1)S闭合,回路中的总电阻为:R总=3Ω
当ab棒匀速下滑时,电动势为:$I=\frac{BLV}{R_总}$
棒中的感应电流为:$I=\frac{BLV}{R_总}$
总电功率为:P总=I2R总
重力的功率为:PG=mgvsinθ
据题设条件有:${I^2}{R_总}=\frac{3}{4}mgvsinθ$
解得:$I=\frac{{\sqrt{mgvsinθ}}}{2}$=2A
B=6T;
(2)设导体棒ab与导轨间的滑动摩擦力为f,由能量守恒有:
$fv=\frac{1}{4}mgvsinθ$
解得:$f=\frac{1}{4}mgsinθ=2N$
$Q=\frac{3}{4}mgsinθ•x-\frac{1}{2}m{v^2}$
解得:$Q=\frac{3}{4}mgsinθ•x-\frac{1}{2}m{v^2}$=4J
(3)S断开后,回路中的总电阻为:R'总=2R1=4Ω
设这一过程经历的时间为△t,通过导体棒ab的平均感应电流为:$q=\bar I△t=\frac{△Φ}{R_总}=\frac{BLx}{R_总}$,
导体棒ab下滑的距离为x,则得:$q=\bar I△t=\frac{△Φ}{R_总}=\frac{BLx}{R_总}$
解得:x=0.8m
(4)断开开关S时,电路总电阻变大,总电流变小,导体棒受到的安培力减小,
所以导体棒将做加速运动.而随着速度增大,感应电动势增大,电流增大,
因此运动过程中导体棒受到的安培力不断增大,合外力减小,加速度减小.
故断开开关S后,电路总电阻变大,导体棒做加速度减小的变加速运动.
断开开关S时:$I′=\frac{BLv}{{R}_{总}^{′}}=\frac{6×0.5×2}{4}A$=1.5A
${F_安}=B{I^'}L=6×1.5×0.5N=4.5N$
${a_1}=\frac{{mgsinθ-f-{F_安}}}{m}=\frac{8-2-4.5}{1.6}m/{s^2}=\frac{15}{16}m/{s^2}=0.9375m/{s^2}$
经过一段时间,合力为零,加速度为零,导体棒做匀速运动.
$mgsinθ=f+\frac{{B}^{2}{L}^{2}{v}_{m}^{′}}{{R}_{总}^{′}}$
解得:${v}_{m}^{′}=\frac{(mgsinθ-f){R}_{总}^{′}}{{B}^{2}{L}^{2}}$=$\frac{8}{3}m/s$≈2.67m/s;
答:(1)匀强磁场的磁感应强度B的大小6T和达到稳定状态后导体棒ab中的电流强度2A;
(2)在这一过程中回路中产生的电热是4J;
(3)这段距离是0.8m;
(4)断开S后导体棒ab的运动性质做加速度减小的变加速运动,最终速度为2.67m/s.
点评 解答本题关键是通过分析功率关系,求出磁感应强度和摩擦力,是电磁感应与电路结合的题目,明确电路的结构解决问题.同时,对于感应电量,要很熟练地根据法拉第电磁感应定律、欧姆定律和电量公式q=It进行推导,并掌握安培力与速度关系式.


 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:填空题
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 在冬季,剩有半瓶热水的暖水瓶经过一个夜晚后,第二天拔瓶口的软木塞时觉得很紧,不易拔出,是因为白天气温升高,大气压强变大 | |
| B. | 一定质量的理想气体,先等温膨胀,再等压压缩,其体积必小于起始体积 | |
| C. | 布朗运动就是液体分子的运动 | |
| D. | 在轮胎爆裂这一短暂过程中,气体膨胀,温度下降 |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
 如图一矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动,右端通过电刷a,b与一平行水平金属板相连接.已知线圈匝数为N=10匝,线圈面积S=0.5m2,线圈匀速转动的转速为n=60r/min,线圈内阻不计,磁场的磁感应强度B=$\frac{10}{π}$(T).平行金属板板长l=0.1m,板间距离d=0.2m,求:
如图一矩形线圈在匀强磁场中绕垂直于磁场的轴OO′匀速转动,右端通过电刷a,b与一平行水平金属板相连接.已知线圈匝数为N=10匝,线圈面积S=0.5m2,线圈匀速转动的转速为n=60r/min,线圈内阻不计,磁场的磁感应强度B=$\frac{10}{π}$(T).平行金属板板长l=0.1m,板间距离d=0.2m,求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题
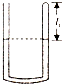 一端封闭的粗细均匀的U形管,用水银封闭一定质量的空气(可看成理想气体),当管内空气温度为t1=31℃时,U型管两边水银面等高,如图所示,此时空气柱长l1=8cm,(设大气压强恒为p0=76cmHg)求:
一端封闭的粗细均匀的U形管,用水银封闭一定质量的空气(可看成理想气体),当管内空气温度为t1=31℃时,U型管两边水银面等高,如图所示,此时空气柱长l1=8cm,(设大气压强恒为p0=76cmHg)求:查看答案和解析>>
科目:高中物理 来源: 题型:解答题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 6m/s | B. | 2$\sqrt{3}$m/s | C. | 3m/s | D. | 3$\sqrt{3}$m/s |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | F可能对物块做正功 | B. | 物块的位移可能为零 | ||
| C. | 物块动量的变化一定为零 | D. | 物块可能做匀速直线运动 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com