
分析 (1)根据万有引力提供向心力即可求出“天宫一号”的周期;
(2)根据题意知,地球表面的重力加速度等于半径为R的球体在表面产生的加速度,深度为d的地球内部的重力加速度相当于半径为R-d的球体在其表面产生的重力加速度,根据地球质量分布均匀得到加速度的表达式,再根据半径关系求解深度为d处的重力加速度与地面重力加速度的比值.卫星绕地球做圆周运动时,运用万有引力提供向心力可以解出高度为h处的加速度,再求其比值.
解答 解:(1)根据万有引力提供向心力得:
$\frac{GMm}{(R+h)^{2}}=\frac{m4{π}^{2}}{{T}^{2}}(R+h)$
地球表面的物体受到的万有引力等于重力,即:
mg=$\frac{GMm}{{R}^{2}}$
联立解得:T=$2π\sqrt{\frac{(R+h)^{3}}{g{R}^{2}}}$
(2)令地球的密度为ρ,对地球表面的物体:g=$\frac{GM}{{R}^{2}}$
由于地球的质量为:M=ρ•$\frac{4}{3}π{R}^{3}$,所以重力加速度的表达式可写成:g=$\frac{GM}{{R}^{2}}$=$\frac{G•ρ\frac{4}{3}π{R}^{3}}{{R}^{2}}$=$\frac{4}{3}$πGρR.
根据万有引力提供向心力$\frac{GMm}{{(R+h)}^{2}}=m{g}_{1}$,“天宫一号”的加速度为${g}_{1}=\frac{GM}{{(R+h)}^{2}}$
$\frac{{g}_{1}}{g}=\frac{{R}^{2}}{{(R+h)}^{2}}$
根据题意有,质量分布均匀的球壳对壳内物体的引力为零,固在深度为d的地球内部,受到地球的万有引力即为半径等于(R-d)的球体在其表面产生的万有引力,故海底的重力加速度g2=$\frac{4}{3}$πGρ(R-d).
所以有$\frac{{g}_{2}}{g}=\frac{R-d}{R}$
所以$\frac{{g}_{2}}{{g}_{1}}=\frac{(R-d){(R+h)}^{2}}{{R}^{3}}$,
答:(1)“天宫一号”绕地心转一周的时间是$2π\sqrt{\frac{(R+h)^{3}}{g{R}^{2}}}$;
(2)“蛟龙”号所在处与“天宫一号”所在处的重力加速度之比为$\frac{(R-d){(R+h)}^{2}}{{R}^{3}}$.
点评 抓住在地球表面重力和万有引力相等,在地球内部,地球的重力和万有引力相等,要注意在地球内部距离地面d处所谓的地球的质量不是整个地球的质量而是半径为(R-d)的球体的质量.


 孟建平错题本系列答案
孟建平错题本系列答案 超能学典应用题题卡系列答案
超能学典应用题题卡系列答案科目:高中物理 来源: 题型:多选题
| A. | 所有行星都在同一椭圆轨道上绕太阳运动 | |
| B. | 行星绕太阳运动时,行星位于椭圆轨道的焦点上 | |
| C. | 离太阳越近的行星,公转周期越短 | |
| D. | 所有行星轨道半长轴的三次方跟公转周期的二次方的比值都相等 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
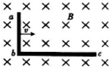 如图所示,水平桌面上放置电阻不计、长度分别为l1、l2(l2>l1)的直金属棒ab和bc连接而成的直角金属架,金属架处于磁感应强度大小为B、方向竖直向下的匀强磁场中.当金属架以速率v沿着bc方向匀速移动时,直角金属架两端的电压为( )
如图所示,水平桌面上放置电阻不计、长度分别为l1、l2(l2>l1)的直金属棒ab和bc连接而成的直角金属架,金属架处于磁感应强度大小为B、方向竖直向下的匀强磁场中.当金属架以速率v沿着bc方向匀速移动时,直角金属架两端的电压为( )| A. | Bl1v | B. | Bl2v | C. | B(l1+l2)v | D. | B(l2-l1)v |
查看答案和解析>>
科目:高中物理 来源: 题型:解答题
查看答案和解析>>
科目:高中物理 来源: 题型:填空题

查看答案和解析>>
科目:高中物理 来源: 题型:选择题
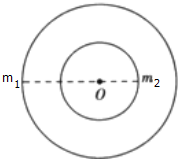 某双星系统由两颗恒星构成,质量分别为m1和m2,距中心距离分别为r1和r2,且r1>r2,则下面的表述正确的是( )
某双星系统由两颗恒星构成,质量分别为m1和m2,距中心距离分别为r1和r2,且r1>r2,则下面的表述正确的是( )| A. | 它们的角速度相同 | B. | 它们的线速度相同 | ||
| C. | m1>m2 | D. | 它们的加速度相同 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | $\frac{R′}{R}$g0 | B. | $\frac{ρ′}{ρ}$g0 | C. | $\frac{R′ρ′}{Rρ}$g0 | D. | $\frac{Rρ}{R′ρ′}$g0 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 若摆长变为原来的$\frac{1}{4}$,则周期变为1s | |
| B. | 若摆球的质量减为原来的$\frac{1}{4}$,则周期变为1s | |
| C. | 若振幅减为原来的$\frac{1}{4}$,则周期变为1s | |
| D. | 若重力加速度减为原来的$\frac{1}{4}$,则周期不变 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
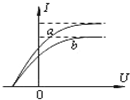 用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )
用同一光电管研究a、b两种单色光产生的光电效应,得到光电流I与光电管两极间所加电压U的关系如图.则这两种光( )| A. | 两种光在光电管内的波长关系为λa>λb | |
| B. | 照射该光电管时a光使其逸出的光电子最大初动能大 | |
| C. | 实验中a的光的强度大于b光 | |
| D. | a光光子能量大于b光光子能量 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com