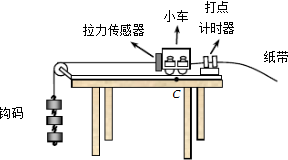
(2012?昌平区二模)(1)某实验小组利用拉力传感器和打点计时器探究“动能定理”,如图1示,他们将拉力传感器固定在小车上,用不可伸长的细线将其通过一个定滑轮与钩码相连,用拉力传感器记录小车受到拉力的大小,在小车的后面连接纸带,通过打点计时器记录小车的运动情况,小车中可以放置砝码.请把下面的实验步骤补充完整.
实验主要步骤如下:
①测量
小车
小车
、砝码和拉力传感器的总质量M,把细线的一端固定在拉力传感器上,另一端通过定滑轮与钩码相连,将纸带连接小车并通过打点计时器,正确连接所需电路.
②将小车停在C点,在释放小车
之前
之前
(选填“之前”或“之后”)接通打点计时器的电源,在纸带上打出一系列的点,记录细线拉力.
③在小车中增加砝码,或减少砝码,重复②的操作.
④处理数据.
实验结果发现小车动能的增加量△E
k总是明显小于拉力F做的功W,你认为其主要原因应该是上述实验步骤中缺少的步骤是
平衡摩擦力
平衡摩擦力
.
(2)小明同学为测量某金属丝的电阻率,他截取了其中的一段,用米尺测出金属丝的长度L,用螺旋测微器测得其直径为D,用多用电表粗测其电阻约为R.
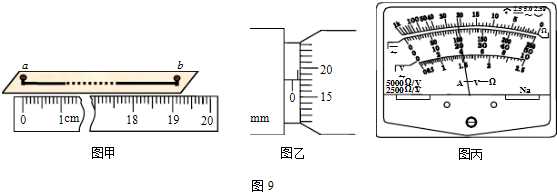
①该同学将米尺的0刻度线与金属丝的左端对齐,从图2甲)中读出金属丝的长度L=
190.0
190.0
mm.
②该同学用螺旋测微器测金属丝的直径,从图2乙)中读出金属丝的直径D=
0.680
0.680
mm.
③该同学选择多用电表“×10”档粗测金属丝的电阻,从图2丙)中读出金属丝的电阻R=
220
220
Ω.
④接着,该同学用伏安法尽可能精确地测出该金属丝的电阻,然后根据电阻定律计算出该金属丝的电阻率.实验室提供的器材有:
A.直流电源E(电动势4V,内阻不计)
B.电流表A
1(量程0~3mA,内阻约50Ω)
C.电流表A
2(量程0~15mA,内阻约30Ω)
D.电压表V
1(量程0~3V,内阻10kΩ)
E.电压表V
2(量程0~15V,内阻25kΩ)
F.滑动变阻器R
1(阻值范围0~15Ω,允许通过的最大电流2.0A)
G.滑动变阻器R
2(阻值范围0~2kΩ,允许通过的最大电流0.5A)
H.待测电阻丝R
x,开关、导线若干
要求较准确地测出其阻值,电流表应选
C
C
,电压表应选
D
D
,滑动变阻器应选
F
F
.(用器材前的字母表示即可)
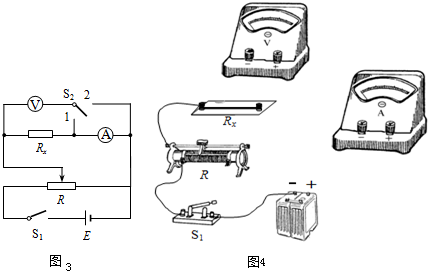
⑤用图3示的电路进行实验测得R
x,实验时,开关S
2应向
1
1
闭合(选填“1”或“2”).
⑥请根据选定的电路图,在如图4示的实物上画出连线(部分线已画出).
⑦(多选)在下列测定金属丝的电阻率的几个步骤中,错误的是
AF
AF
.
A.先用米尺测出金属丝的长度,再将金属丝两端固定在接线柱上悬空拉直;
B.用螺旋测微器在不同位置测出金属丝的直径D各三次,求平均值
;
C.打开开关,将选好的实验器材按图3接成实验电路;
D.闭合开关,调节滑动变阻器,使电流表和电压表有合适的示数,读出并记下这组数据;
E.改变滑动变阻器的滑键位置,重复进行实验,测出6组数据,并记录在表格中;
F.分别计算出电流平均值(
)和电压的平均值(
),再求出电阻的平均值
=;
G.根据电阻定律计算出该金属丝的电阻率.
⑧设金属丝的长度为L(m),直径的平均值为
(m),电阻的平均值为
(Ω),则该金属丝电阻率的表达式为ρ=
.




 名校课堂系列答案
名校课堂系列答案 (2012?昌平区二模)在如图所示的电路中,电源电动势为E、内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光.当滑动变阻器的滑片向右移动时,下列判断正确的是( )
(2012?昌平区二模)在如图所示的电路中,电源电动势为E、内电阻为r,C为电容器,R0为定值电阻,R为滑动变阻器.开关闭合后,灯泡L能正常发光.当滑动变阻器的滑片向右移动时,下列判断正确的是( ) (2012?昌平区二模)一列简谐横波,在t=6.0s时的波形如图(甲)所示,图(乙)是这列波中质点P的振动图线,那么该波的传播速度和传播方向是( )
(2012?昌平区二模)一列简谐横波,在t=6.0s时的波形如图(甲)所示,图(乙)是这列波中质点P的振动图线,那么该波的传播速度和传播方向是( )

