
如图所示,![]() 、
、![]() 、
、![]() 为三个质点,
为三个质点,![]() 的质量远远大于
的质量远远大于![]() 、
、![]() 的质量,
的质量,![]() 和
和![]() 的质量相等。已知
的质量相等。已知![]() 、
、![]() 之间,
之间,![]() 、
、![]() 之间存在相互吸引力。
之间存在相互吸引力。![]() 、
、![]() 之间存在相互排斥力,三个把质点在相互间引力或斥力的作用下运动,如果作用力合适,可以存在一种如下形式的运动:
之间存在相互排斥力,三个把质点在相互间引力或斥力的作用下运动,如果作用力合适,可以存在一种如下形式的运动:
A、![]() 、
、![]() 的相对位置固定,它们构成一个平面,三个质点绕着位于这个平面内的某条轴匀速转动;因为质点
的相对位置固定,它们构成一个平面,三个质点绕着位于这个平面内的某条轴匀速转动;因为质点![]() 的质量远远大于
的质量远远大于![]() 、
、![]() 的质量,可认为该轴过质点
的质量,可认为该轴过质点![]() 且固定不动;连线
且固定不动;连线![]() 与转轴的夹角
与转轴的夹角![]() 与连线
与连线![]() 与转轴的夹角
与转轴的夹角![]() 不相等,且
不相等,且![]() ,
,![]() 。
。
若![]() 之间吸引力的大小
之间吸引力的大小![]() ,
,![]() 之间吸引力的大小为
之间吸引力的大小为![]() ,其中
,其中![]() 、
、![]() 分别为
分别为![]() 、
、![]() 与
与![]() 、
、![]() 之间的距离,
之间的距离,![]() 为比例系数,不计重力的影响。试问
为比例系数,不计重力的影响。试问![]() 的值在什么范围内,上述运动才能实现?
的值在什么范围内,上述运动才能实现?

解法1:
以![]() 表示质点
表示质点![]() 的质点,
的质点,![]() 表示连线
表示连线![]() 与竖直方向的夹角,
与竖直方向的夹角,![]() 表示转动角速度,
表示转动角速度,![]() 表示
表示![]() 间排斥力的大小。根据牛顿定律有
间排斥力的大小。根据牛顿定律有
![]() , (1)
, (1)
![]() , (2)
, (2)
![]() , (3)
, (3)
![]() 。 (4)
。 (4)
由(1)、(3)两式并利用(2)、(4)两式可得
![]() 。 (5)
。 (5)
考虑到几何关系
![]() (6)
(6)
并利用已知![]() 和
和![]() 的表示式。可由(5)得到
的表示式。可由(5)得到
![]() (7)
(7)
又,由(2)、(4)式可得![]() 。 (8)
。 (8)
带入已知的![]() 和
和![]() 的表达式可得
的表达式可得
![]() 。 (9)
。 (9)
联立(7)、(9)从而有
![]() 。 (10)
。 (10)
如果![]() ,则意味着方程
,则意味着方程
![]() (11)
(11)
在![]() 区间有两个不同的解,其中
区间有两个不同的解,其中![]() 为某一合适的常数。这要求函数
为某一合适的常数。这要求函数![]() 在
在![]() 区间不能是单调函数,也就是说
区间不能是单调函数,也就是说![]() 和
和![]() 不能同时为单调增函数或单调减函数。因此当
不能同时为单调增函数或单调减函数。因此当![]() 增大时,若
增大时,若![]() 增大,则
增大,则![]() 应减小;反之,若
应减小;反之,若![]() 减小,则
减小,则![]() 应增大,故
应增大,故![]() 与
与![]() 同号。因此有
同号。因此有
![]() (12)
(12)
![]() 。 (13)
。 (13)
对![]() ,可知
,可知![]() 在
在![]() 及
及![]() 时均为零,因此
时均为零,因此![]() 在
在![]() 区间一定存在极值点,意味着方程(11)在
区间一定存在极值点,意味着方程(11)在![]() 合适选取的情况下必有两个或两个以上的不同解。对
合适选取的情况下必有两个或两个以上的不同解。对![]() 亦然。因此条件(12)、(13)是符合题意要求的充分必要条件。
亦然。因此条件(12)、(13)是符合题意要求的充分必要条件。
评分标准:(1)~(4)式各1分,(6)式1分,(10)式6分,(12)、(13)式及其以下说明共4分。
解法2:
如图,设![]() 、
、![]() 间的排斥力是
间的排斥力是![]() ,它们受到
,它们受到![]() 的吸引力分别是
的吸引力分别是![]() 、
、![]() ,向心力分别是
,向心力分别是![]() 、
、![]() ,距离
,距离![]() 分别是
分别是![]() 、
、![]() ;根据三角形的相似关系,有
;根据三角形的相似关系,有
![]() , (1a)
, (1a)
![]() 。 (2a)
。 (2a)
以上两式相比可得
![]() (3a)
(3a)
依题意有
![]() , (4a)
, (4a)
![]() , (5a)
, (5a)
![]() , (6a)
, (6a)
将(4a)~(6a)代入(3a)得
![]() 。 (7a)
。 (7a)
由(7a)得
![]() 。 (8a)
。 (8a)
之后的讨论与“参考解答1”相同。
评分标准:考虑“参考解答1”。




 阅读快车系列答案
阅读快车系列答案科目:高中物理 来源: 题型:
| πm |
| 2qB0 |
| 11 |
| 3 |
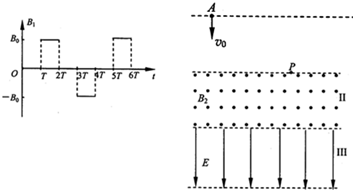
查看答案和解析>>
科目:高中物理 来源: 题型:
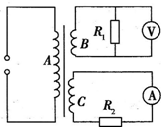 如图所示,理想变压器有三个线圈A、B、C,其中B、C的匝数分别为n2、n3电压表的示数为U,电流表的示数为I,R1、R2是完全相同的电阻,根据以上条件可以计算出的物理量是( )
如图所示,理想变压器有三个线圈A、B、C,其中B、C的匝数分别为n2、n3电压表的示数为U,电流表的示数为I,R1、R2是完全相同的电阻,根据以上条件可以计算出的物理量是( )查看答案和解析>>
科目:高中物理 来源: 题型:
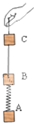 如图所示,完全相同的三个木块,A、B之间用轻弹簧相连,B、C之间用不可伸长的轻杆相连,在手的拉动下,木块间达到稳定后,一起向上做匀减速运动,加速度大小为5m/s2.某一时刻突然放手,则在手释放的瞬间,三个木块的加速度下列说法正确的是(以向上为正方向,g取10m/s2)( )
如图所示,完全相同的三个木块,A、B之间用轻弹簧相连,B、C之间用不可伸长的轻杆相连,在手的拉动下,木块间达到稳定后,一起向上做匀减速运动,加速度大小为5m/s2.某一时刻突然放手,则在手释放的瞬间,三个木块的加速度下列说法正确的是(以向上为正方向,g取10m/s2)( )| A、aA=0,aB=aC=-5m/s2 | B、aA=-5m/s2,aB=aC=-12.5m/s2 | C、aA=-5m/s2,aB=-15m/s2,aC=-10m/s2 | D、aA=-5m/s2,aB=aC=-5m/s2 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com