
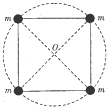
 宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.如图,设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为L的正方形的四个顶点上.已知引力常量为G,关于四星系统(忽略星体自转的影响),下列说法正确的是( )
宇宙中存在一些质量相等且离其他恒星较远的四颗星组成的四星系统,通常可忽略其他星体对它们的引力作用.如图,设四星系统中每个星体的质量均为m,半径均为R,四颗星稳定分布在边长为L的正方形的四个顶点上.已知引力常量为G,关于四星系统(忽略星体自转的影响),下列说法正确的是( )| A. | 四颗星的向心加速度的大小为$\frac{2\sqrt{2}Gm}{{L}^{2}}$ | |
| B. | 四颗星运行的线速度大小是$\sqrt{\frac{Gm(1+2\sqrt{2})}{2\sqrt{2}L}}$ | |
| C. | 四颗星表面的重力加速度均为G$\frac{m}{{R}^{2}}$ | |
| D. | 四颗星的周期均为2πL$\sqrt{\frac{2L}{Gm(1+2\sqrt{2})}}$ |
分析 在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的引力的合力提供圆周运动的向心力,根据合力提供向心力,求出星体匀速圆周运动的加速度、线速度和周期.在星球表面上,根据万有引力等于重力,求出星体表面的重力加速度.
解答 解:任一星体在其他三个星体的万有引力作用下围绕正方形对角线的交点做匀速圆周运动,轨道半径均r=$\frac{\sqrt{2}}{2}L$,
根据$\frac{G{m}^{2}}{(\sqrt{2}L)^{2}}+\frac{\sqrt{2}G{m}^{2}}{{L}^{2}}=ma$=m$\frac{{v}^{2}}{r}$=m$r\frac{4{π}^{2}}{{T}^{2}}$得,a=$\frac{(2\sqrt{2}+1)Gm}{2{L}^{2}}$,v=$\sqrt{\frac{Gm}{L}(1+\frac{\sqrt{2}}{4})}$=$\sqrt{\frac{Gm(1+2\sqrt{2})}{2\sqrt{2}L}}$,T=2πL$\sqrt{\frac{2L}{(4+\sqrt{2})Gm}}$,故A、D错误,B正确.
根据$G\frac{{m}^{2}}{{R}^{2}}=mg$得,星球表面的重力加速度g=$\frac{Gm}{{R}^{2}}$,故C正确.
故选:BC.
点评 解决本题的关键掌握万有引力等于重力,以及知道在四颗星组成的四星系统中,其中任意一颗星受到其它三颗星对它的合力提供圆周运动的向心力.


科目:高中物理 来源: 题型:计算题
查看答案和解析>>
科目:高中物理 来源: 题型:计算题
 如图所示,AB为水平皮带传送装置的两端,物体与皮带的动摩擦因数为0.2,在A端质量为m=1kg的物体以v=5m/s的速度滑上皮带,皮带立即以3m/s2的加速度从静止开始向右匀加速运动,物块经3s到达B点.
如图所示,AB为水平皮带传送装置的两端,物体与皮带的动摩擦因数为0.2,在A端质量为m=1kg的物体以v=5m/s的速度滑上皮带,皮带立即以3m/s2的加速度从静止开始向右匀加速运动,物块经3s到达B点.查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 根据速度定义式v=$\frac{△x}{△t}$,当△t→0时,$\frac{△x}{△t}$就可以表示物体在t时刻的瞬时速度,该定义运用了极限思维法 | |
| B. | 电场强度是用比值法定义的,因而不能说成电场强度与电场力成正比,与电量成反比 | |
| C. | 奥斯特受法拉第发现电流的磁效应的启发发现了电磁感应现象 | |
| D. | 卡文迪许在利用扭秤实验装置测量万有引力常量时,应用了放大法 |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
| A. | 登陆舱在r1与r2轨道上运动时的速度大小之比为$\frac{v_1}{v_2}=\sqrt{\frac{{{m_1}{r_2}}}{{{m_2}{r_1}}}}$ | |
| B. | 登陆舱在半径为r2轨道上做圆周运动的周期为${T_2}={T_1}\sqrt{\frac{{{r_2}^3}}{{{r_1}^3}}}$ | |
| C. | X星球表面的重力加速度为${g_x}=\frac{{4{π^2}{r_1}}}{T_1^2}$ | |
| D. | X星球的质量为$M=\frac{{4{π^2}r_1^3}}{GT_1^2}$ |
查看答案和解析>>
科目:高中物理 来源: 题型:多选题
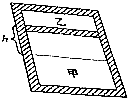 如图所示,汽缸放置在水平地面上,质量为m的活塞将汽缸分成甲、乙两气室,两气室中均充有气体.汽缸、活塞是绝热的且不漏气.开始时活寒被销钉固定,现将销钉拨掉,活塞最终静止在距原位置下方h处,设活塞移动前后甲气室内气体内能的变化量为△U,不计气体重心改变的影响,下列说法正确的是( )
如图所示,汽缸放置在水平地面上,质量为m的活塞将汽缸分成甲、乙两气室,两气室中均充有气体.汽缸、活塞是绝热的且不漏气.开始时活寒被销钉固定,现将销钉拨掉,活塞最终静止在距原位置下方h处,设活塞移动前后甲气室内气体内能的变化量为△U,不计气体重心改变的影响,下列说法正确的是( )| A. | △U<mgh | |
| B. | △U>mgh | |
| C. | 甲气室内气体温度升高,乙气室内气体温度降低 | |
| D. | 乙气室内气体内能的减小量等于甲气室内气体内能的增加量 | |
| E. | 乙气室内气体内能的减小量小于甲气室内气体内能的增加量 |
查看答案和解析>>
科目:高中物理 来源: 题型:选择题
| A. | 做曲线运动的物体.受到的合外力大小一定变化 | |
| B. | 在平衡力作用下的物体,可以做曲线运动 | |
| C. | 只要物体做圆周运动,它所受的合外力一定指向圆心 | |
| D. | 做曲线运动的物体,受到的合外力方向可能始终保持不变 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com